题目内容
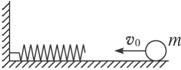
如图16-6-8所示，光滑水平面上一轻弹簧，左端固定在竖直挡板上，自然伸长，其劲度系数为k，一质量为m的小球以速度v0由右向左运动与弹簧接触并压缩弹簧，最后被弹簧向右反弹出去，小球与弹簧接触的时间为t，求这段时间内弹簧弹力的冲量和平均弹力各为多大？
图16-6-8
2mv0，方向向右 
，方向向右
解析:
弹簧在压缩过程中产生的弹力是变化的，直接用冲量公式I=Ft无法求得该力冲量，故我们只能用动量定理求解，用动量定理求出的力是变力在这段时间内的平均力，以向左为正方向，初速度为v0方向向左，故p1=mv0.
根据机械能守恒定律，小球被反弹后的动能与初动能相同，即Ek=
mv′2=mv02，得v′=v0，方向向右，为负值，故p2=-mv0
设弹力冲量为I，这段时间内的平均弹力为F，则根据动量定理有I=Δp=p2-p1=-mv0-mv0=-2mv0
由Ft=Δp得F=
，负号表示方向向右.
练习册系列答案
考前必练系列答案
相关题目
中的球投进离地面高3 m的吊环，他在车上和车一起以2 m/s的速度向吊环运动，小朋友抛球时手离地面1.2 m，当他在离吊环的水平距离为2 m时将球相对于自己竖直上抛，球刚好进入吊环，他将球竖直向上抛出时的速度是(g取10 m/s2)( )