题目内容
【题目】如图所示,两根足够长的光滑平行直导轨AB、CD与水平面成θ角放置,两导轨间距为L,A、C两点间接有阻值为R的定值电阻.一根质量为m、长也为L的均匀直金属杆ef放在两导轨上,并与导轨垂直.整套装置处于磁感应强度为B的匀强磁场中,磁场方向垂直于导轨平面向上,导轨和金属杆接触良好,金属杆ef的电阻为r,其余部分电阻不计.现让ef杆由静止开始沿导轨下滑.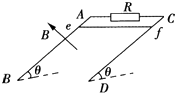
(1)求ef杆下滑的最大速度vm .
(2)已知ef杆由静止释放至达到最大速度的过程中,ef杆沿导轨下滑的距离为x,求此过程中定值电阻R产生的焦耳热Q和在该过程中通过定值电阻R的电荷量q.
【答案】
(1)解:根据法拉第电磁感应定律和安培力公式有:
E=BLv ①
I= ![]() ②
②
FA=BIL ③
根据牛顿第二定律有:
mgsinθ﹣FA=ma ④
联立①②③④得:mgsinθ﹣ ![]() =ma
=ma
当加速度a为零时,速度v达最大,速度最大值:vm= ![]() ,
,
故ef杆下滑的最大速度为:vm= ![]() .
.
答:ef杆下滑的最大速度vm为 ![]() .
.
(2)解:根据能量守恒定律有:
mgxsinθ= ![]() mvm2+Q总.
mvm2+Q总.
得 Q总=mgxsinθ﹣ ![]()
定值电阻R产生的焦耳热 Q= ![]() Q总=
Q总= ![]() [mgxsinθ﹣
[mgxsinθ﹣ ![]() ]
]
根据电磁感应定律有: ![]() =
= ![]()
根据闭合电路欧姆定律有: ![]() =
= ![]()
感应电量:q= ![]() △t=
△t= ![]() =
= ![]()
答:此过程中定值电阻R产生的焦耳热Q是[mgxsinθ﹣ ![]() ],在该过程中通过定值电阻R的电荷量q为
],在该过程中通过定值电阻R的电荷量q为 ![]() .
.
【解析】(1)首先分析杆的运动:杆的速度逐渐变大,安培力将逐渐变大,所以杆在导轨上做加速度逐渐减小的加速运动,当安培力等于重力沿导轨分力时匀速运动,速度达到最大.(2)杆下滑过程中,重力势能减小转化为电路中的焦耳热和杆的动能,因此根据功能关系可求出焦耳热;根据法拉第电磁感应定律求出平均电流,然后根据q=It即可求出电量.
【考点精析】根据题目的已知条件,利用电磁感应现象和电磁感应与电路的相关知识可以得到问题的答案,需要掌握电磁感应现象的实质是产生感应电动势,如果回路闭合,则有感应电流,回路不闭合,则只有感应电动势而无感应电流;用法拉第电磁感应定律和楞次定律确定感应电动势的大小和方向;画等效电路;运用全电路欧姆定律,串并联电路性质,电功率等公式联立求解.

【题目】某课外学习小组想描绘标有“4V、2W”的小灯泡的U﹣I图象,除导线和开关外还备有以下器材可供选择:
A.电流表(量程0.6A,内阻约为1Ω)
B.电流表(量程3.0A,内阻约为0.2Ω)
C.电压表(量程5.0V,内阻约为5kΩ)
D.电压表(量程15.0V,内阻约为15kΩ)
E.滑动变阻器(最大阻值为200Ω,额定电流100mA)
F.滑动变阻器(最大阻值为10Ω,额定电流1.0A)
G.电源(电动势为6.0V,内阻约为1.5Ω)
(1)实验中所用的电流表应选;电压表应选;滑动变阻器应选 . (只需填器材前面的字母代号)
(2)将图甲中的实物连接成实验所需的电路(有两根导线已经接好) . 实验开始时,滑动变阻器的滑片应该置于最端.(填“左”或“右”)
(3)经过正确的操作,测得的数据如下表:
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
U/V | 0 | 0.4 | 0.8 | 1.2 | 1.6 | 2.0 | 2.4 | 2.8 | 3.2 | 3.6 | 4.0 |
I/A | 0 | 0.12 | 0.22 | 0.30 | 0.36 | 0.40 | 0.43 | 0.46 | 0.48 | 0.49 | 0.50 |
请在图乙中描点画出小灯泡的U﹣I曲线.
(4)若某干电池的端电压U与电流I的关系如图乙中图线a所示,那么将本题中的小灯泡接在该干电池的两端时,小灯泡的实际功率是W.