题目内容
 斜面固定在水平地面上,倾角θ=53°,斜面足够长,物体与斜面间的动摩擦因数μ=0.8,如图所示.一物体以v0=6.4m/s的初速度从斜面底端向上滑行,sin53°=0.8,cos53°=0.6,g取10m/s2,求
斜面固定在水平地面上,倾角θ=53°,斜面足够长,物体与斜面间的动摩擦因数μ=0.8,如图所示.一物体以v0=6.4m/s的初速度从斜面底端向上滑行,sin53°=0.8,cos53°=0.6,g取10m/s2,求(1)物体上滑的最大距离
(2)物体返回斜面底端的时间
(3)物体运动到最大高度一半时的速度.
分析:(1)根据动能定理求解物体上滑的最大距离.
(2)根据牛顿第二定律求出物体下滑过程的加速度大小,由位移公式x=
at2求出物体返回斜面底端的时间.
(3)根据动能定理求解物体运动到最大高度一半时的速度,分上滑和下滑两个过程研究.
(2)根据牛顿第二定律求出物体下滑过程的加速度大小,由位移公式x=
| 1 |
| 2 |
(3)根据动能定理求解物体运动到最大高度一半时的速度,分上滑和下滑两个过程研究.
解答:解:(1)物体上滑过程,根据动能定理得
-(mgxsinθ+μmgcosθ)x=0-
m
解得,x=1.6m
(2)根据牛顿第二定律得,物体下滑过程的加速度大小为a=
=g(sinθ-μcosθ)
代入解得,a=3.2m/s2.
由x=
at2得,t=
=1s
(3)设上滑和下滑到最大高度一半时物体的速度大小分别为v1和v2,则
上滑:-(mgxsinθ+μmgcosθ)
x=
m
-
m
下滑:(mgxsinθ-μmgcosθ)
x=
m
解得,v1=3.2
m/s,v2=1.6
m/s.
答:
(1)物体上滑的最大距离是1.6m.
(2)物体返回斜面底端的时间是1s.
(3)物体上滑到最大高度一半时的速度为3.2
m/s,下滑到最大高度一半时的速度为1.6
m/s.
-(mgxsinθ+μmgcosθ)x=0-
| 1 |
| 2 |
| v | 2 0 |
解得,x=1.6m
(2)根据牛顿第二定律得,物体下滑过程的加速度大小为a=
| mgsinθ-μmgcosθ |
| m |
代入解得,a=3.2m/s2.
由x=
| 1 |
| 2 |
|
(3)设上滑和下滑到最大高度一半时物体的速度大小分别为v1和v2,则
上滑:-(mgxsinθ+μmgcosθ)
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 0 |
下滑:(mgxsinθ-μmgcosθ)
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 2 |
解得,v1=3.2
| 2 |
| 2 |
答:
(1)物体上滑的最大距离是1.6m.
(2)物体返回斜面底端的时间是1s.
(3)物体上滑到最大高度一半时的速度为3.2
| 2 |
| 2 |
点评:本题是两个过程的问题,运用动能定理、牛顿第二定律和运动学规律结合进行处理,还要抓住两个过程的位移大小相等.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
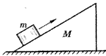 如图所示,一个倾角为θ的斜面固定在水平地面上,质量为m的物块与斜面之间的动摩擦因数为μ.并以某一初速度沿劈的斜面向上滑,至速度为零后静止在斜面上.则下列选项中正确的是( )
如图所示,一个倾角为θ的斜面固定在水平地面上,质量为m的物块与斜面之间的动摩擦因数为μ.并以某一初速度沿劈的斜面向上滑,至速度为零后静止在斜面上.则下列选项中正确的是( )| A、物块在上滑过程中所受摩擦力大小为mgsinθ | B、物块在上滑过程中所受摩擦力大小为μmg | C、物块m静止在斜面上后,所受的摩擦力大小为μmgcosθ | D、物块m静止在斜面上后,所受的摩擦力大小为mgsinθ |
 如图甲所示,表面绝缘、倾角θ=30°的斜面固定在水平地面上,斜面的顶端固定有弹性挡板,挡板垂直于斜面,并与斜面底边平行.斜面所在空间有一宽度D=0.40m的匀强磁场区域,其边界与斜面底边平行,磁场方向垂直斜面向上,磁场上边界到挡板的距离s=0.55m.一个质量m=0.10kg、总电阻R=0.25Ω的单匝矩形闭合金属框abcd,放在斜面的底端,其中ab边与斜面底边重合,ab边长L=0.50m.从t=0时刻开始,线框在垂直cd边沿斜面向上大小恒定的拉力作用下,从静止开始运动,当线框的ab边离开磁场区域时撤去拉力,线框继续向上运动,并与挡板发生碰撞,碰撞过程的时间可忽略不计,且没有机械能损失.线框向上运动过程中速度与时间的关系如图乙所示.已知线框在整个运动过程中始终未脱离斜面,且保持ab边与斜面底边平行,线框与斜面之间的动摩擦因数μ=
如图甲所示,表面绝缘、倾角θ=30°的斜面固定在水平地面上,斜面的顶端固定有弹性挡板,挡板垂直于斜面,并与斜面底边平行.斜面所在空间有一宽度D=0.40m的匀强磁场区域,其边界与斜面底边平行,磁场方向垂直斜面向上,磁场上边界到挡板的距离s=0.55m.一个质量m=0.10kg、总电阻R=0.25Ω的单匝矩形闭合金属框abcd,放在斜面的底端,其中ab边与斜面底边重合,ab边长L=0.50m.从t=0时刻开始,线框在垂直cd边沿斜面向上大小恒定的拉力作用下,从静止开始运动,当线框的ab边离开磁场区域时撤去拉力,线框继续向上运动,并与挡板发生碰撞,碰撞过程的时间可忽略不计,且没有机械能损失.线框向上运动过程中速度与时间的关系如图乙所示.已知线框在整个运动过程中始终未脱离斜面,且保持ab边与斜面底边平行,线框与斜面之间的动摩擦因数μ=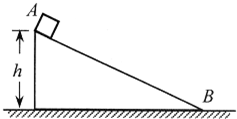 如图所示,高为h的光滑斜面固定在水平地面上.一质量为m的小物块,从斜面顶端A由静止开始下滑.重力加速度为g,不计空气阻力.求:
如图所示,高为h的光滑斜面固定在水平地面上.一质量为m的小物块,从斜面顶端A由静止开始下滑.重力加速度为g,不计空气阻力.求: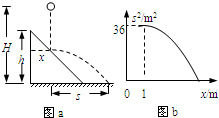 如图a所示,倾角为45°、高为h的斜面固定在水平地面上,小球从高为H(2h>H>h)的某处自由下落,与斜面碰撞(无能量损失)后做平抛运动.若小球做平抛运动后能直接落到水平地面上,自由下落的起始点距斜面左端的水平距离x应满足的条件是
如图a所示,倾角为45°、高为h的斜面固定在水平地面上,小球从高为H(2h>H>h)的某处自由下落,与斜面碰撞(无能量损失)后做平抛运动.若小球做平抛运动后能直接落到水平地面上,自由下落的起始点距斜面左端的水平距离x应满足的条件是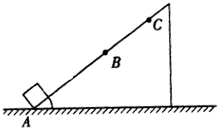 如图所示,足够长斜面固定在水平地面上.可视为质点的物体在外界作用下,以加速度a1从A点由静止开始运动,到达B点时加速度突变为a2,且方向与a1相反,物体继续运动到达C点时速度为零.整个运动过程经仪器测量并采集三个时刻物体瞬时速度情况如下:0.2s末速度为1.2m/s,1.8s末速度为6.0m/s,2.0s末速度为4.0m/s.(以开始运动为计时零点).试通过上述信息求:
如图所示,足够长斜面固定在水平地面上.可视为质点的物体在外界作用下,以加速度a1从A点由静止开始运动,到达B点时加速度突变为a2,且方向与a1相反,物体继续运动到达C点时速度为零.整个运动过程经仪器测量并采集三个时刻物体瞬时速度情况如下:0.2s末速度为1.2m/s,1.8s末速度为6.0m/s,2.0s末速度为4.0m/s.(以开始运动为计时零点).试通过上述信息求: