题目内容
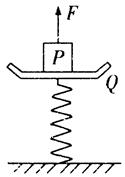
 一个弹簧秤放在水平地面上,Q为与轻弹簧上端连在一起的秤盘,P为重物,已知P的质量M=10.5kg,Q 的质量m=1.5kg,弹簧的质量不计,劲度系数k=800N/m,系统处于静止.如图所示,现给P施加一个方向竖直向上的力F,使它从静止开始向上做匀加速运动,已知在前0.2s内,F为变力,0.2s以后,F为恒力.
一个弹簧秤放在水平地面上,Q为与轻弹簧上端连在一起的秤盘,P为重物,已知P的质量M=10.5kg,Q 的质量m=1.5kg,弹簧的质量不计,劲度系数k=800N/m,系统处于静止.如图所示,现给P施加一个方向竖直向上的力F,使它从静止开始向上做匀加速运动,已知在前0.2s内,F为变力,0.2s以后,F为恒力.求:力F的最大值与最小值.(取 g=10m/s 2 )
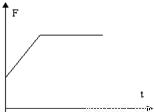
分析:在P、Q分离之前F为变力,分离后,F为恒力;两物体分离瞬间,P对Q无作用力,但Q的加速度恰好与原来一样,此后Q的加速度将减小,而从开始到分离历时0.2s,由分析可知,刚开始时F最小,F为恒力时最大
解答:解:设刚开始时弹簧压缩亮为x1,则:
x1=
=0.15m①
设两者刚好分离时,弹簧压缩量为x2,则对Q:
kx2-mg=ma②
在前0.2s时间内,有运动学公式得:
x1-x2=
at2③
由①②③解得:a=6m/s2
由牛顿第二定律得,
开始时,Fmin=(M+m)a=72N
最终分离后,Fmax-Mg=Ma
即:Fmax=M(g+a)=168N
答:力F最小为72N,最大为168N
x1=
| (m+M)g |
| k |
设两者刚好分离时,弹簧压缩量为x2,则对Q:
kx2-mg=ma②
在前0.2s时间内,有运动学公式得:
x1-x2=
| 1 |
| 2 |
由①②③解得:a=6m/s2
由牛顿第二定律得,
开始时,Fmin=(M+m)a=72N
最终分离后,Fmax-Mg=Ma
即:Fmax=M(g+a)=168N
答:力F最小为72N,最大为168N
点评:弹簧的弹力是变力,分析好何时两者分离是关键,此时两者间无作用力,且两者加速度刚好相等,另外牛顿定律与运动学公式的熟练应用也是同学必须掌握的

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
 (2011?泗阳县一模)一个弹簧秤放在水平地面上,Q为与轻弹簧上端连在一起的秤盘,P为重物,已知P的质量M=10.5kg,Q的质量 m=1.5kg,弹簧的质量不计,劲度系数 k=800N/m,系统处于静止.如图所示,现给P施加一个方向竖直向上的力F,使它从静止开始向上做匀加速运动,则在向上运动的过程中力F随时间变化的图象是( )
(2011?泗阳县一模)一个弹簧秤放在水平地面上,Q为与轻弹簧上端连在一起的秤盘,P为重物,已知P的质量M=10.5kg,Q的质量 m=1.5kg,弹簧的质量不计,劲度系数 k=800N/m,系统处于静止.如图所示,现给P施加一个方向竖直向上的力F,使它从静止开始向上做匀加速运动,则在向上运动的过程中力F随时间变化的图象是( )