题目内容
(选修模块3-4)
(1)A、B、C是三个完全相同的时钟,A放在地面上,B、C分别放在两个火箭上,以速度vb和vc朝同一方向飞行,vb>vc.在地面上的人看来,关于时钟快慢的说法正确的是
A.B钟最快,C钟最慢 B.A钟最快,C钟最慢
C.C钟最快,B钟最慢 D.A钟最快,B钟最慢
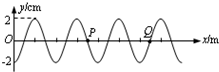
(2)如图1所示,实线是一列简谐横波在t1=0时的波形图,虚线为t2=0.5s时的波形图,已知0<t2-t1<T,t1=0时,x=2m处的质点A正向y轴正方向振动.
①波速大小为
②从t2时刻计时,x=1m处的质点的振动方程是
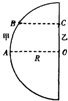
(3)如图2所示,半圆玻璃砖的半径R=10cm,折射率为n=
,直径AB与屏幕垂直并接触于A点.激光a以入射角i=30°射向半圆玻璃 砖的圆心O,结果在水平屏幕MN上出现两个光斑.求两个光斑之间的距离L.

(1)A、B、C是三个完全相同的时钟,A放在地面上,B、C分别放在两个火箭上,以速度vb和vc朝同一方向飞行,vb>vc.在地面上的人看来,关于时钟快慢的说法正确的是
D
D
A.B钟最快,C钟最慢 B.A钟最快,C钟最慢
C.C钟最快,B钟最慢 D.A钟最快,B钟最慢
(2)如图1所示,实线是一列简谐横波在t1=0时的波形图,虚线为t2=0.5s时的波形图,已知0<t2-t1<T,t1=0时,x=2m处的质点A正向y轴正方向振动.
①波速大小为
2m/s
2m/s
;②从t2时刻计时,x=1m处的质点的振动方程是
y=-5sinπt(cm)
y=-5sinπt(cm)
.(3)如图2所示,半圆玻璃砖的半径R=10cm,折射率为n=
| 3 |

分析:(1)根据相对论效应分析钟的快慢.
(2)①根据t1=0时,x=2m处的质点A的振动方向确定波的传播方向,根据波形的平移法求出在t2-t1时间内波传播的距离,求出波速.②由图读出波长和振幅,求出周期.分析t2时刻x=1m处的质点的状态,写出振动方程.
(3)作出光路图,根据折射定律和几何知识求解两个光斑之间的距离L.
(2)①根据t1=0时,x=2m处的质点A的振动方向确定波的传播方向,根据波形的平移法求出在t2-t1时间内波传播的距离,求出波速.②由图读出波长和振幅,求出周期.分析t2时刻x=1m处的质点的状态,写出振动方程.
(3)作出光路图,根据折射定律和几何知识求解两个光斑之间的距离L.
解答: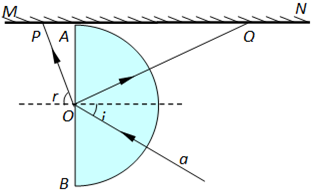 解:(1)B、C两钟放在两个火箭上,根据爱因斯坦相对论可知,B、C变慢,由于vb>vc,B钟比C钟更慢,所以A钟最快,B钟最慢.
解:(1)B、C两钟放在两个火箭上,根据爱因斯坦相对论可知,B、C变慢,由于vb>vc,B钟比C钟更慢,所以A钟最快,B钟最慢.
故选D
(2)①由题,t1=0时,x=2m处的质点A正向y轴正方向振动,则波沿x轴正方向传播.因为0<t2-t1<T,波向右传播为距离为△x=
λ=1m
则波速为 v=
=
m/s=2m/s
②t2时刻x=1m处的质点经过平衡位置向下,周期T=
=
s=2s,角速度ω=
=πrad/s,从t2时刻计时,x=1m处的质点的振动方程是y=-5sinπt cm.
(3)画出如图光路图,设折射角为r,根据折射定律 n=
代入解得 r=60°
由几何知识得,△OPQ为直角三角形,
所以两个光斑PQ之间的距离 L=PA+AQ=Rtan30°+2Rsin60°
解得 L=
≈23.1cm
故答案为:
(1)D;(2)①2m/s;②y=-5sinπt(cm);(3)两个光斑之间的距离L为23.1cm.
 解:(1)B、C两钟放在两个火箭上,根据爱因斯坦相对论可知,B、C变慢,由于vb>vc,B钟比C钟更慢,所以A钟最快,B钟最慢.
解:(1)B、C两钟放在两个火箭上,根据爱因斯坦相对论可知,B、C变慢,由于vb>vc,B钟比C钟更慢,所以A钟最快,B钟最慢.故选D
(2)①由题,t1=0时,x=2m处的质点A正向y轴正方向振动,则波沿x轴正方向传播.因为0<t2-t1<T,波向右传播为距离为△x=
| 1 |
| 4 |
则波速为 v=
| △v |
| △t |
| 1 |
| 0.5 |
②t2时刻x=1m处的质点经过平衡位置向下,周期T=
| λ |
| v |
| 4 |
| 2 |
| 2π |
| T |
(3)画出如图光路图,设折射角为r,根据折射定律 n=
| sinr |
| sini |
代入解得 r=60°
由几何知识得,△OPQ为直角三角形,
所以两个光斑PQ之间的距离 L=PA+AQ=Rtan30°+2Rsin60°
解得 L=
40
| ||
| 3 |
故答案为:
(1)D;(2)①2m/s;②y=-5sinπt(cm);(3)两个光斑之间的距离L为23.1cm.
点评:第1题要理解记住爱因斯坦相对论效应之一:钟慢效应.简谐波的图象波形平移法是常用的方法.几何光学要正确作出光路图,这是分析和计算的基础.

练习册系列答案
相关题目


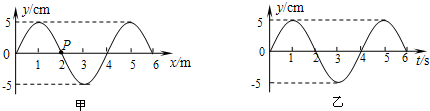 (2)图甲为某一简谐横波在t=0时刻的波动图象,P为其传播方向上的一个质点,图乙为质点P的振动图象.根据图象可知:波的传播速度为
(2)图甲为某一简谐横波在t=0时刻的波动图象,P为其传播方向上的一个质点,图乙为质点P的振动图象.根据图象可知:波的传播速度为