题目内容
7. 如图所示,光滑水平面上有一平板车,车上固定一竖直直杆,杆的最高点O通过一长为L的轻绳拴接一个可视为质点的小球,小球的质量为小车(包括杆的质量)质量的一半,悬点O距离地面的高度为2L,轻绳水平时,小球与小车速度均为零.释放小球,当小球运动到最低点时.求:(重力加速度为g)
如图所示,光滑水平面上有一平板车,车上固定一竖直直杆,杆的最高点O通过一长为L的轻绳拴接一个可视为质点的小球,小球的质量为小车(包括杆的质量)质量的一半,悬点O距离地面的高度为2L,轻绳水平时,小球与小车速度均为零.释放小球,当小球运动到最低点时.求:(重力加速度为g)(ⅰ)小球运动到最低点时速度大小;
(ⅱ)小球从释放到最低点的过程中,小车向右移动的距离.
分析 (i)小球在下落过程中,小球与车组成的系统水平方向动量守恒;而系统机械能守恒;则由动量守恒定律和机械能守恒定律列式可求得小球的速度;
(ii)对小球和小车系统根据平均动量守恒定律可确定位移关系.
解答 解:( i)小球下落过程中,小球与车组成的系统,水平方向动量守恒,系统机械能守恒,设小球到最低点时,小球的速率为v1,小车的速率为v2,设小球的速度方向为正方向,则由机械能守恒定律和动量守恒可得:
m v1=2m v2
mgL=$\frac{1}{2}$mv12+$\frac{1}{2}$×2mv22
解得:v1=$\frac{2\sqrt{3gL}}{3}$,v2=$\frac{\sqrt{3gL}}{3}$
故可得小球在最低点的速度为:v1=$\frac{2\sqrt{3gL}}{3}$;
( ii)小球下落的过程中,车向右移动的距离为x2,小球向左移动的距离为x1,则有:
m x1=2mx2
且x1+x2=L
所以,小车向右运动的位移为:x2=$\frac{1}{3}$L
答:(ⅰ)小球运动到最低点时速度大小为$\frac{2\sqrt{3gL}}{3}$;
(ⅱ)小球从释放到最低点的过程中,小车向右移动的距离为$\frac{1}{3}L$.
点评 以动量守恒定律的应用为命题背景考查学生的推理能力和分析综合能力;要求能正确分析物理过程及受力情况,再根据相对应的物理模型选择正确的物理规律.

练习册系列答案
相关题目
18.我们经常在电视中看到男、女花样滑冰运动员手拉手在冰面上旋转并表演各种优美的动作.现有甲、乙两名花样滑冰运动员,M甲=80kg,M乙=40kg,他们面对面拉着弹簧测力计各自以他们连线上某一点为圆心做匀速圆周运动,若两人相距0.9m,弹簧测力计的示数为600N,则( )
| A. | 两人的线速度相同,为0.4 m/s | |
| B. | 两人的角速度相同,为5.0 rad/s | |
| C. | 两人的运动半径相同,都是0.45 m | |
| D. | 两人的运动半径不同,甲的半径是0.3m、乙的半径是0.6 m |
15.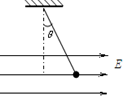 如图所示,质量为m,电量为q的带正电的小球,用长度为l的轻绳悬挂在天花板上,未加电场时轻绳在竖直方向,当加水平向右的匀强电场后,小球向外偏转的最大角度θ=37°.则电场强度E的大小为( )
如图所示,质量为m,电量为q的带正电的小球,用长度为l的轻绳悬挂在天花板上,未加电场时轻绳在竖直方向,当加水平向右的匀强电场后,小球向外偏转的最大角度θ=37°.则电场强度E的大小为( )
 如图所示,质量为m,电量为q的带正电的小球,用长度为l的轻绳悬挂在天花板上,未加电场时轻绳在竖直方向,当加水平向右的匀强电场后,小球向外偏转的最大角度θ=37°.则电场强度E的大小为( )
如图所示,质量为m,电量为q的带正电的小球,用长度为l的轻绳悬挂在天花板上,未加电场时轻绳在竖直方向,当加水平向右的匀强电场后,小球向外偏转的最大角度θ=37°.则电场强度E的大小为( )| A. | $\frac{mg}{3q}$ | B. | $\frac{3mg}{4q}$ | C. | $\frac{5mg}{4q}$ | D. | $\frac{4mg}{3q}$ |
2.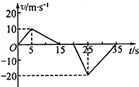 质量m=50kg的某同学站在观光电梯地板上,用速度传感器记录了电梯在一段时间内运动的速度随时间变化情况(以竖直向上为正方向).由图象提供的信息可知( )
质量m=50kg的某同学站在观光电梯地板上,用速度传感器记录了电梯在一段时间内运动的速度随时间变化情况(以竖直向上为正方向).由图象提供的信息可知( )
 质量m=50kg的某同学站在观光电梯地板上,用速度传感器记录了电梯在一段时间内运动的速度随时间变化情况(以竖直向上为正方向).由图象提供的信息可知( )
质量m=50kg的某同学站在观光电梯地板上,用速度传感器记录了电梯在一段时间内运动的速度随时间变化情况(以竖直向上为正方向).由图象提供的信息可知( )| A. | 在0~15s内,观光电梯上升的高度为25m | |
| B. | 在5~15s内,电梯内的同学处于超重状态 | |
| C. | 在20~25s与25~35s内,观光电梯的平均速度大小均为10m/s | |
| D. | 在25~35s内,观光电梯在减速上升,该同学的加速度大小2m/s2 |
19.两个物体做匀速圆周运动,在相同的时间内,它们通过的路程之比为4:3,运动方向改变的角度之比为3:2,它们的向心加速度之比为( )
| A. | 2:1 | B. | 1:2 | C. | 8:9 | D. | 9:8 |
17.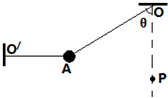 两根不计伸缩的轻质细线,将它们分别固定在O、O′点,另一端固定在可视为质点的质量为m的小球A上.如图所示,其中θ=60°,OA长为L,O′A水平,P为在悬点的正下方水平固定的一枚钉子,OP距离为$\frac{3L}{4}$(保证能使小球下摆时其细线能碰到P).现剪断水平细线O′A,A球开始下摆(在以后的运动中细线OA能承受的力足够大),则下列说法正确的有( )
两根不计伸缩的轻质细线,将它们分别固定在O、O′点,另一端固定在可视为质点的质量为m的小球A上.如图所示,其中θ=60°,OA长为L,O′A水平,P为在悬点的正下方水平固定的一枚钉子,OP距离为$\frac{3L}{4}$(保证能使小球下摆时其细线能碰到P).现剪断水平细线O′A,A球开始下摆(在以后的运动中细线OA能承受的力足够大),则下列说法正确的有( )
 两根不计伸缩的轻质细线,将它们分别固定在O、O′点,另一端固定在可视为质点的质量为m的小球A上.如图所示,其中θ=60°,OA长为L,O′A水平,P为在悬点的正下方水平固定的一枚钉子,OP距离为$\frac{3L}{4}$(保证能使小球下摆时其细线能碰到P).现剪断水平细线O′A,A球开始下摆(在以后的运动中细线OA能承受的力足够大),则下列说法正确的有( )
两根不计伸缩的轻质细线,将它们分别固定在O、O′点,另一端固定在可视为质点的质量为m的小球A上.如图所示,其中θ=60°,OA长为L,O′A水平,P为在悬点的正下方水平固定的一枚钉子,OP距离为$\frac{3L}{4}$(保证能使小球下摆时其细线能碰到P).现剪断水平细线O′A,A球开始下摆(在以后的运动中细线OA能承受的力足够大),则下列说法正确的有( )| A. | 水平细线O′A剪断后的瞬间,OA细线拉力为$\frac{mg}{2}$ | |
| B. | 水平细线O′A剪断后的瞬间,小球A的加速度方向水平向右 | |
| C. | 细线碰到P后的瞬间,OA细线拉力为5mg | |
| D. | 细线碰到P后恰能作完整的圆周运动 |

 如图所示,半径为R=1.00m的水平光滑圆桌面,不可伸长的柔软轻绳一端固定在圆心O处,另一端系质量为m=7.5×10-2kg的小物块(图中未画出).将小物块放在桌面上并将绳拉直,当给小物块一个方向与绳垂直、大小为v0=4m/s的初速度时,刚好将轻绳拉断,已知轻绳能承受的最大张力为T0=2N.求:
如图所示,半径为R=1.00m的水平光滑圆桌面,不可伸长的柔软轻绳一端固定在圆心O处,另一端系质量为m=7.5×10-2kg的小物块(图中未画出).将小物块放在桌面上并将绳拉直,当给小物块一个方向与绳垂直、大小为v0=4m/s的初速度时,刚好将轻绳拉断,已知轻绳能承受的最大张力为T0=2N.求: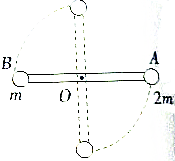 如图所示,在一长为2L不可伸长的轻杆两端各固定一质量为2m与m的小球A、B,系统可绕过轻杆的中点且垂直纸面的固定转轴O转动,初始时轻杆处于水平状态,无初速度释放后轻杆转动,当轻杆转至竖直位置时,求小球A的速率.
如图所示,在一长为2L不可伸长的轻杆两端各固定一质量为2m与m的小球A、B,系统可绕过轻杆的中点且垂直纸面的固定转轴O转动,初始时轻杆处于水平状态,无初速度释放后轻杆转动,当轻杆转至竖直位置时,求小球A的速率.