��Ŀ����
13�� Ϊ����С������ˮƽ�����Ķ�Ħ��������ijС���������ͼ��ʵ��װ�ã����е���ɹ̶��������ϣ��ᵯ������뵲��������������Ϊh��O1��O2��A��B��C���������ͬһˮƽֱ���ϣ���֪�������ٶ�Ϊg�����������ɺ��Բ��ƣ�ʵ������£�
Ϊ����С������ˮƽ�����Ķ�Ħ��������ijС���������ͼ��ʵ��װ�ã����е���ɹ̶��������ϣ��ᵯ������뵲��������������Ϊh��O1��O2��A��B��C���������ͬһˮƽֱ���ϣ���֪�������ٶ�Ϊg�����������ɺ��Բ��ƣ�ʵ������£�����һ����ͼ�ף�����̶���01�㣬��С����ŵ������ϣ������ƶ�����ѹ�����ɣ������Ƶ�A��������O1A�ľ��룬�������ɾ�ֹ�ͷţ������뿪���������ˮƽ�����ϵ�P�㣬���P�㵽�����Ҷ˵�ˮƽ����Ϊx1��
���̶���������Ĺ̶����Ƶ���O1��Ϊd��O2�㣬��ͼ�ң��ƶ�����ѹ�����ɣ������Ƶ�C����ʹO2C=O1A���������ɾ�ֹ�ͷţ������뿪���������ˮƽ�����ϵ�Q�㣬���Q�㵽�����Ҷ˵�ˮƽ����Ϊx2�����������գ�
��1��Ϊ��ɱ�ʵ�飬����˵����ȷ����C��
A��������С��������� B�����������ɵľ���ϵ��
C�����ɵ�ѹ��������̫С D�����������ɵ�ԭ��
��2��д����Ħ�������ı���ʽ��=$\frac{{{x}_{1}}^{2}-{{x}_{2}}^{2}}{4dh}$�������������������ķ��ű�ʾ����
��3����֪ʵ���õĦ�ֵ��ʵ��ֵƫ����ԭ�����ʵ���в���������⣬�������ܵ�ԭ���ǻ����ܿ��������ȣ�д��һ�����ɣ���
��4��ijͬѧ��Ϊ������������߶ȣ�����������С������뿪���浽��ص�ʱ�䣬Ҳ�ɲ��С������ˮƽ�����Ķ�Ħ�����������ַ��������У�ѡ����С������С����������ǻ����ڿ��з���ʱ��̣ܶ������ʱ�����ϴ�
���� ��ʵ������IJ����֪����������µ������Ĺ���ȣ���黬������ʱ�Ķ����ǵ���������Ħ���������ĺͣ�������黬����ͬ�����µ�Ħ�������Ĺ����������Ħ�����Ĵ�С��Ħ�������Ĵ�С��
��� �⣺��1��2�������뿪�������ƽ���˶���ƽ���˶���ʱ�䣺t=$\sqrt{\frac{2h}{g}}$��
������еľ��룺x=v•t
���Ի����1���뿪����ʱ���ٶȣ�${v}_{1}={x}_{1}\sqrt{\frac{g}{2h}}$��
�����2���뿪����ʱ���ٶȣ�${v}_{2}={x}_{2}\sqrt{\frac{g}{2h}}$��
�����1�λ����Ĺ����У����ɵĵ�����Ħ�����������赯�����Ĺ���W1��AB֮��ľ�����x����
${W}_{1}-��mgx=\frac{1}{2}m{{v}_{1}}^{2}$��
�����1�λ����Ĺ����У�W1-��mg•��x+d�� ��
�����٢ڢۢܿɵã�$��mgd=\frac{1}{2}m��{{v}_{2}}^{2}-{{v}_{1}}^{2}��$��
��æ�=$\frac{{{x}_{1}}^{2}-{{x}_{2}}^{2}}{4dh}$��
��֪��Ҫ�ⶨĦ���������뵯�ɵij��ȡ����ɵľ���ϵ�����Լ�������������أ�Ҫ���û���˳���������棬���ɵ�ѹ��������̫С����C��ȷ��
��ѡ��C��
��3��ʵ���õĦ�ֵ��ʵ��ֵƫ����ԭ�����ʵ���в���������⣬�������ܵ�ԭ���ǻ����ܵ������������õȣ�
��4������������С����ӷ������浽��ص�ʱ�䣬���ⶨС������ˮƽ�����Ķ�Ħ����������ʵ�鷽���Dz����еģ�ԭ���� �����ڿ��з���ʱ��̣ܶ������ռ�ʱ�����յ㣬�����ʱ�����ϴ�
�ʴ�Ϊ����1��C����2��$\frac{{{x}_{1}}^{2}-{{x}_{2}}^{2}}{4dh}$����3�������ܿ��������ȣ���4�������У������ڿ��з���ʱ��̣ܶ������ʱ�����ϴ�
���� ���ʵ����������Ҫ���ո�ʵ��ԭ�����˽�ʵ��IJ�����������ݴ����Լ�ע�����ͬʱҪ����Ӧ����ѧ�������ɽ��ʵ�����⣮

 ��У����ϵ�д�
��У����ϵ�д� ��ͼ��ʾ��������ĵ���������ԭ��������
��ͼ��ʾ��������ĵ���������ԭ�������� ���ο�ǻ������⣬����Dz��ӵأ�ȡ����Զ������Ϊ�㣮������
���ο�ǻ������⣬����Dz��ӵأ�ȡ����Զ������Ϊ�㣮������| A�� | A ��糡ǿ��Ϊ�� | B�� | A ��糡ǿ�Ȳ�Ϊ�� | ||
| C�� | A �����Ϊ�� | D�� | A �����С���� |
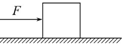 ��ͼ��ʾ����F�������£�����Ϊm�������������˶�����֪����������Ķ�Ħ������Ϊ�̣��������������Ħ������С����������˵����������ȷ���ǣ�������
��ͼ��ʾ����F�������£�����Ϊm�������������˶�����֪����������Ķ�Ħ������Ϊ�̣��������������Ħ������С����������˵����������ȷ���ǣ�������| A�� | f=0 | B�� | f=��mg | C�� | f=F | D�� | f=��mg-F |
| A�� | �г�����ʱ�ٶ�Ϊ�㣬�����ٶ�ҲΪ�� | |
| B�� | ������ʻ�Ĵ������г����������ٶȺܴ����Լ��ٶȺܴ� | |
| C�� | ���ٶ���Сʱ������һ�������ȼ����˶� | |
| D�� | ���ٶ����˶�������ͬʱ������һ�����������˶� |
 ijͬѧ����֤ţ�ٵڶ����ɵ�ʵ�飬ʹ�õ������У������ֵij�ľ�塢С������С���ϰڷŵĴ����롢ϸ�ߡ�СͰ����СͰ��ŵ�С���롢����ʱ���ȣ�
ijͬѧ����֤ţ�ٵڶ����ɵ�ʵ�飬ʹ�õ������У������ֵij�ľ�塢С������С���ϰڷŵĴ����롢ϸ�ߡ�СͰ����СͰ��ŵ�С���롢����ʱ���ȣ�
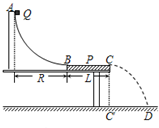 ����С���Q��ƽ��P֮��Ķ�Ħ��������ʵ��װ����ͼ��ʾ��AB�ǰ뾶�㹻��ġ��⻬���ķ�֮һԲ���������ˮƽ�̶����õ�P����ϱ���BC��B�����У�C����ˮƽ����Ĵ�ֱͶӰΪC�䣮�������ٶ�Ϊg��ʵ�鲽�����£�
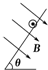
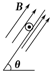
����С���Q��ƽ��P֮��Ķ�Ħ��������ʵ��װ����ͼ��ʾ��AB�ǰ뾶�㹻��ġ��⻬���ķ�֮һԲ���������ˮƽ�̶����õ�P����ϱ���BC��B�����У�C����ˮƽ����Ĵ�ֱͶӰΪC�䣮�������ٶ�Ϊg��ʵ�鲽�����£�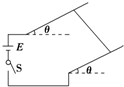 ��ͼ��ʾ���⻬��ƽ�е������Դ���Ӻ���ˮƽ����ɦȽ���б���ã������Ϸ�һ������Ϊm�Ľ������������S�պϺ��ڰ����������ڼ�һ�����ʵ���ǿ�ų�������ʹ�������ֹƽ�⣬�����ĸ�ͼ�зֱ���˲�ͬ����Ĵų������п���ƽ����ǣ�������
��ͼ��ʾ���⻬��ƽ�е������Դ���Ӻ���ˮƽ����ɦȽ���б���ã������Ϸ�һ������Ϊm�Ľ������������S�պϺ��ڰ����������ڼ�һ�����ʵ���ǿ�ų�������ʹ�������ֹƽ�⣬�����ĸ�ͼ�зֱ���˲�ͬ����Ĵų������п���ƽ����ǣ�������