题目内容
17. 如图,光滑水平面上两个体积相同的小球A和B静止在同一直线上,B球右侧有一固定的竖直挡板.现小球A以速度v0=3m/s向右运动并与B球发生弹性正碰.已知A球的质量为mA=1kg,B球与挡板挡板碰撞无机械能损失.则:
如图,光滑水平面上两个体积相同的小球A和B静止在同一直线上,B球右侧有一固定的竖直挡板.现小球A以速度v0=3m/s向右运动并与B球发生弹性正碰.已知A球的质量为mA=1kg,B球与挡板挡板碰撞无机械能损失.则:①若碰后B球的速度大小为vB=2m/s,求B球的质量mB;
②若全过程A和B只能发生一次碰撞,求B球的质量应满足的条件.
分析 ①A、B碰撞过程系统动量守恒,应用动量守恒定律可以求出B的质量.
②A、B碰撞过程系统动量守恒,如果A、B只能发生一次碰撞,则A、B碰撞后A的速度大小应大于B的速度大小,应用动量守恒定律求出B的质量应满足的条件.
解答 解:①A、B发生弹性碰撞,碰撞过程动量守恒,A、B系统动量守恒,以向右为正方向,由动量守恒定律得:
mAv0=mAvA+mBvB,
由机械能守恒定律得:$\frac{1}{2}$mAv02=$\frac{1}{2}$mAvA2+$\frac{1}{2}$mBvB2,
代入数据解得:mB=2kg;
②B与挡板碰撞没有机械能损失,则B与挡板碰撞后返回而速度大小不变,
A、B碰撞过程系统动量守恒,如果A、B只能发生一次碰撞,
A、B碰撞后A的速度大小应大于B的速度大小,且碰撞后A应反向,即:vA≥vB,
A、B发生弹性碰撞,碰撞过程动量守恒,机械能守恒,
A、B系统动量守恒,以向右为正方向,由动量守恒定律得:
mAv0=-mAvA+mBvB,
由机械能守恒定律得:$\frac{1}{2}$mAv02=$\frac{1}{2}$mAvA2+$\frac{1}{2}$mBvB2,
解得:vB=$\frac{6}{{m}_{B}+1}$,vA=mBvB-3,
A、B只发生一次碰撞需要满足:vA≥vB,
解得:mB≥3kg;
答:①若碰后B球的速度大小为vB=2m/s,求B球的质量mB为2kg;
②若全过程A和B只能发生一次碰撞,B球的质量应满足的条件是mB≥3kg.
点评 本题考查了动量守恒定律的应用,分析清楚球的运动过程,应用动量守恒定律与机械能守恒定律即可解题;分析清楚两球只发生一次碰撞的条件是正确解题的关键.

练习册系列答案
相关题目
7. 如图所示的双缝干涉实验,用绿光照射单缝S时,在光屏P上观察到干涉条纹.要得到相邻条纹间距更大的干涉图样,可以( )
如图所示的双缝干涉实验,用绿光照射单缝S时,在光屏P上观察到干涉条纹.要得到相邻条纹间距更大的干涉图样,可以( )
 如图所示的双缝干涉实验,用绿光照射单缝S时,在光屏P上观察到干涉条纹.要得到相邻条纹间距更大的干涉图样,可以( )
如图所示的双缝干涉实验,用绿光照射单缝S时,在光屏P上观察到干涉条纹.要得到相邻条纹间距更大的干涉图样,可以( )| A. | 增大S1与S2的间距 | B. | 减小双缝屏到光屏的距离 | ||
| C. | 将绿光换为红光 | D. | 将绿光换为紫光 |
8.下列关于功的说法中正确的是( )
| A. | 由于功有正负,所以功是矢量 | |
| B. | 计算式W=FScosα中,F是力的大小,S是位移的大小,α是力F和位移S的夹角 | |
| C. | 合力对物体做的功,等于各分力做功的矢量和 | |
| D. | 功的单位是瓦特 |
5. 如图所示,质量为M的三角形滑块置于水平光滑的地面上,斜面亦光滑,当质量为m的滑块沿斜面下滑的过程中,M与m组成的系统( )
如图所示,质量为M的三角形滑块置于水平光滑的地面上,斜面亦光滑,当质量为m的滑块沿斜面下滑的过程中,M与m组成的系统( )
 如图所示,质量为M的三角形滑块置于水平光滑的地面上,斜面亦光滑,当质量为m的滑块沿斜面下滑的过程中,M与m组成的系统( )
如图所示,质量为M的三角形滑块置于水平光滑的地面上,斜面亦光滑,当质量为m的滑块沿斜面下滑的过程中,M与m组成的系统( )| A. | 由于不受摩擦力,系统动量守恒 | |
| B. | 由于地面对系统的支持力大小不等于系统所受重力大小,故系统动量不守恒 | |
| C. | 系统水平方向不受外力,故系统水平方向动量守恒 | |
| D. | M对m作用有水平方向分力,故系统水平方向动量也不守恒 |
4.学习物理除了知识的学习外,还要领悟并掌握处理物理问题的思想与方法.下列关于物理方法说法不正确的是( )
| A. | 元电荷是一种理想化模型 | |
| B. | 电容不是用比值法定义的物理量 | |
| C. | 运动的合成与分解是等效替代的方法 | |
| D. | 库仑定律的发现是类比了万有引力定律的平方反比关系 |
11.在光滑的水平面上,有甲、乙两玩具小车,两小车间夹一轻质弹簧,弹簧仅与两车接触但不连接,用两手握住小车压缩弹簧,并使两小车静止,则( ) (多选)
| A. | 两手同时释放,两小车的总动量不为零 | |
| B. | 先释放甲小车,后释放乙小车,两小车的总动量指向乙小车一方 | |
| C. | 先释放甲小车,后释放乙小车,两小车的总动量指向甲小车一方 | |
| D. | 在先释放甲小车,后释放乙小车的全过程中,两小车的总动量不守恒 |
9.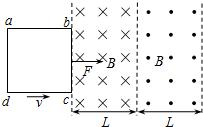 如图所示,两个相邻有界匀强磁场区域,磁场方向相反,且垂直纸面,磁感应强度大小均为B,两个磁场区域宽度均为L.边长为L,总电阻为R的正方形导线框abcd的bc边与磁场边界重合,线框在垂直于bc边的外力F作用下,从图示位置水平向右以速度v匀速运动,线框平面始终保持在纸面内,bc边线始终保持与磁场边界平行.关于线框穿过两磁场区域全过程中的下列说法,正确的是( )
如图所示,两个相邻有界匀强磁场区域,磁场方向相反,且垂直纸面,磁感应强度大小均为B,两个磁场区域宽度均为L.边长为L,总电阻为R的正方形导线框abcd的bc边与磁场边界重合,线框在垂直于bc边的外力F作用下,从图示位置水平向右以速度v匀速运动,线框平面始终保持在纸面内,bc边线始终保持与磁场边界平行.关于线框穿过两磁场区域全过程中的下列说法,正确的是( )
 如图所示,两个相邻有界匀强磁场区域,磁场方向相反,且垂直纸面,磁感应强度大小均为B,两个磁场区域宽度均为L.边长为L,总电阻为R的正方形导线框abcd的bc边与磁场边界重合,线框在垂直于bc边的外力F作用下,从图示位置水平向右以速度v匀速运动,线框平面始终保持在纸面内,bc边线始终保持与磁场边界平行.关于线框穿过两磁场区域全过程中的下列说法,正确的是( )
如图所示,两个相邻有界匀强磁场区域,磁场方向相反,且垂直纸面,磁感应强度大小均为B,两个磁场区域宽度均为L.边长为L,总电阻为R的正方形导线框abcd的bc边与磁场边界重合,线框在垂直于bc边的外力F作用下,从图示位置水平向右以速度v匀速运动,线框平面始终保持在纸面内,bc边线始终保持与磁场边界平行.关于线框穿过两磁场区域全过程中的下列说法,正确的是( )| A. | 线框中感应电流方向始终保持不变 | B. | 线框中感应电流最大值为$\frac{2BLv}{R}$ | ||
| C. | 通过线框横截面的总电量为$\frac{2B{L}^{2}}{R}$ | D. | F做的总功为$\frac{6{B}^{2}{L}^{3}v}{R}$ |
 质量m=1kg的物体,在水平拉力F的作用下,沿粗糙水平面运动,经过位移4m时,拉力F停止作用,接着又运动了位移4m时物体停止,运动过程中物体的动能随位移(Ek-S)的图线如图所示,(g取10m/s2)求:
质量m=1kg的物体,在水平拉力F的作用下,沿粗糙水平面运动,经过位移4m时,拉力F停止作用,接着又运动了位移4m时物体停止,运动过程中物体的动能随位移(Ek-S)的图线如图所示,(g取10m/s2)求: 如图9所示,在磁感应强度B=0.5T的匀强磁场中,让长L=0.2m的导体AB在金属框上以υ=5m/s的速度向右滑动.如果R1=2Ω,R2=1Ω,其他导线上的电阻忽略不计.求通过AB的电流大小.
如图9所示,在磁感应强度B=0.5T的匀强磁场中,让长L=0.2m的导体AB在金属框上以υ=5m/s的速度向右滑动.如果R1=2Ω,R2=1Ω,其他导线上的电阻忽略不计.求通过AB的电流大小.