Question

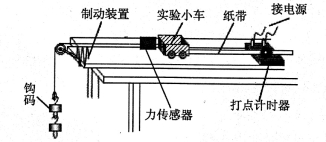
一滑块在桌面上做匀加速直线运动，现用高速摄影机在同一底片上多次曝光，记录滑块运动过程中在每次曝光时的位置，并将滑块的位置编号，得到的照片如图所示。由于底片保管不当，其中位置4处被污损。若已知摄影机连续两次曝光的时间间隔为Δt=1s，则利用该照片可求出：小球运动的加速度约为a=___________m/s2；位置4对应的速度为v=__________m/s；若位置2、位置3、位置5、位置6在刻度尺的位置分别用x2、x3、x5、x6来表示，则位置4在刻度尺的位置为x4=___________（用上述给定的字母表示）。

 

 

Answer 1

（1）3.0×10-2(2.9×10-2～3.1×10-2均可)；9.0×10-2；或

等形式

【解析】

试题分析：因为摄影机连续两次曝光的时间间隔为1s，T=1s

由图可知x56=13.5cm   x23=4.5cm

根据运动学公式△x=at2得x56-x23=3aT2，即．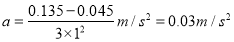

利用匀变速直线运动的推论得：

根据运动学公式△x=at2=恒量得：

x45-x34=at2，

所以x5-x4-（x4-x3）=a△t2

所以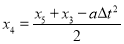

所以可以求出4的具体位置．

考点：研究匀变速运动。