题目内容
【题目】如图所示，一根不可伸长的轻绳跨过光滑的水平轴 O ，两端分别连接质量为m的小球 A 和质量为4m的物块 B ，物块B置于 O 点正下方的水平面上，拉直绳使 OA 水平，此时 OA 的长度为 L 。
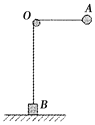
（1）小球 A 由静止释放绕 O 点转过90°时，求小球的速度大小和物块对地面的压力
（2）若保持 A 的质量不变，将 B 换成质量也为m的物块，使绳 OA 水平，当小球 A 由静止释放转到 O 点正下方时，物块 B 的速度大小为v，求小球 A 的速度大小和方向（设 A 与 B 不会相碰，方向用三角函数表示）。
【答案】（1）
、mg 方向竖直向下
（2）
、速度方向与水平向右夹角θ的正弦值
【解析】试题分析：1）对A球，在OA转过90°的过程，设小球A在O点正下方时的速度为v0，由机械能守恒得：
mgL=
mv02
解得： 
A在O点正下方时，设绳对小球A的拉力为T，地面对物块的支持力为NB
对小球有：T-mg=m
解得：T=3mg
绳对物块B的拉力 T′=T=3mg
对物块：NB+T′=mBg
解得：NB=mBg-T′=4mg-3mg=mg
由牛顿第三定律可知，物块B对地面的压力大小 NB′=NB=mg，方向竖直向下．
（2）设小球A在O点正下方时的速度大小为vA，与水平向左方向成θ角斜向下．
对小球A和物块B组成的系统，由机械能守恒有：
mgL=
mv2+
mvA2
解得： 
小球A在O点正下方时速度的竖直分量：vAy=v速度分解如图所示
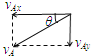
则速度方向与水平向右夹角θ的正弦值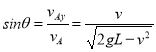
练习册系列答案
阅读快车系列答案
相关题目
