题目内容
5. 如图所示,空中有三个点电荷A,B,C,质量均为m;A和B所带电荷量为+Q,C所带电荷量为-Q,AB连线水平长度为L,C围绕A,B连线中心O在竖直面内作匀速圆周运动,OC之间的距离为$\frac{L}{2}$,不计重力,静电力常量为k,求:
如图所示,空中有三个点电荷A,B,C,质量均为m;A和B所带电荷量为+Q,C所带电荷量为-Q,AB连线水平长度为L,C围绕A,B连线中心O在竖直面内作匀速圆周运动,OC之间的距离为$\frac{L}{2}$,不计重力,静电力常量为k,求:(1)电荷C作圆周运动的向心力;
(2)电荷C运动的角速度.
分析 (1)根据电场强度的叠加原理可求得C点所在的圆弧上的电场强度大小,再由F=EQ可求得向心力;
(2)由向心力公式可求得角速度的大小.
解答 解:单个电荷在C点形成的场强E=$\frac{2kQ}{{L}^{2}}$;
由电场的叠加可知,C点所在的圆弧上的电场强度E总=$\sqrt{2}$E=$\frac{2\sqrt{2}kQ}{{L}^{2}}$;
C球受到的向心力F=E总Q=$\frac{2\sqrt{2}K{Q}^{2}}{{L}^{2}}$;
(2)由向心力公式可知:
F=m$\frac{L}{2}{ω}^{2}$
解得:ω=$\frac{2Q}{L}$$\sqrt{\frac{\sqrt{2}K}{mL}}$
答:(1)电荷C作圆周运动的向心力$\frac{2\sqrt{2}K{Q}^{2}}{{L}^{2}}$;
(2)电荷C运动的角速度$\frac{2Q}{L}$$\sqrt{\frac{\sqrt{2}K}{mL}}$.
点评 本题要注意分析电荷所在位置处的场强大小及方向,解题的关键在于正确分析几何关系,明确电场的叠加原理的应用.

练习册系列答案
相关题目
15.在电梯内的地板上,竖直放置一根轻质弹簧,弹簧上端固定一个质量为m的物体.当电梯匀速运动时,弹簧被压缩了x,某时刻后观察到弹簧又被继续压缩了$\frac{x}{10}$(重力加速度为g).则电梯在此时刻后的运动情况可能是( )
| A. | 以大小为$\frac{11}{10}$g的加速度加速上升 | B. | 以大小为$\frac{11}{10}$g的加速度减速上升 | ||
| C. | 以大小为$\frac{g}{10}$的加速度加速下降 | D. | 以大小为$\frac{g}{10}$的加速度减速下降 |
13.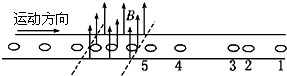 如图所示,通过水平绝缘的传送带输送完全相同的铜线圈,线圈均与传送带以相同的速度匀速运动.为了检测出个别未闭合的不合格线圈,让传送带通过一固定匀强磁场区域,磁场方向垂直于传送带,线圈进入磁场前等距离排列,穿过磁场后根据线圈间的距离,就能够检测出不合格线圈,通过观察图形,判断下列说法正确的是( )
如图所示,通过水平绝缘的传送带输送完全相同的铜线圈,线圈均与传送带以相同的速度匀速运动.为了检测出个别未闭合的不合格线圈,让传送带通过一固定匀强磁场区域,磁场方向垂直于传送带,线圈进入磁场前等距离排列,穿过磁场后根据线圈间的距离,就能够检测出不合格线圈,通过观察图形,判断下列说法正确的是( )
 如图所示,通过水平绝缘的传送带输送完全相同的铜线圈,线圈均与传送带以相同的速度匀速运动.为了检测出个别未闭合的不合格线圈,让传送带通过一固定匀强磁场区域,磁场方向垂直于传送带,线圈进入磁场前等距离排列,穿过磁场后根据线圈间的距离,就能够检测出不合格线圈,通过观察图形,判断下列说法正确的是( )
如图所示,通过水平绝缘的传送带输送完全相同的铜线圈,线圈均与传送带以相同的速度匀速运动.为了检测出个别未闭合的不合格线圈,让传送带通过一固定匀强磁场区域,磁场方向垂直于传送带,线圈进入磁场前等距离排列,穿过磁场后根据线圈间的距离,就能够检测出不合格线圈,通过观察图形,判断下列说法正确的是( )| A. | 若线圈闭合,线圈相对传送带向后滑动 | |
| B. | 若线圈不闭合,线圈相对传送带向后滑动 | |
| C. | 从图中可以看出,第2个线圈是不合格线圈 | |
| D. | 从图中可以看出,第3个线圈是不合格线圈 |
10.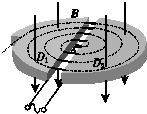 1930年劳伦斯制成了世界上第一台回旋加速器,其原理如图所示.这台加速器由两个铜质D形盒D1、D2构成,其间留有空隙.下列说法正确的是( )
1930年劳伦斯制成了世界上第一台回旋加速器,其原理如图所示.这台加速器由两个铜质D形盒D1、D2构成,其间留有空隙.下列说法正确的是( )
 1930年劳伦斯制成了世界上第一台回旋加速器,其原理如图所示.这台加速器由两个铜质D形盒D1、D2构成,其间留有空隙.下列说法正确的是( )
1930年劳伦斯制成了世界上第一台回旋加速器,其原理如图所示.这台加速器由两个铜质D形盒D1、D2构成,其间留有空隙.下列说法正确的是( )| A. | 离子回旋周期逐渐增大 | B. | 离子回旋周期逐渐减小 | ||
| C. | 离子从磁场中获得能量 | D. | 离子从电场中获得能量 |
17.奥斯特发现了电流的磁效应,由此揭开了电磁学的崭新时代的序幕,以下关于这段电磁学历史描述错误的是( )
| A. | 安培研究了电流间相互作用的规律,并提出了分子电流假说来解释磁现象 | |
| B. | 法拉第发现了电磁感应现象,并且给出了判断电磁感应电流大小和方向的定量规律 | |
| C. | 法拉第在研究电磁现象的过程中,提出了场的观点,认为电磁作用必须借助场作为媒介 | |
| D. | 麦克斯韦继承了法拉第关于场的观点,并进一步研究了电场和磁场的性质 |
15. 如图所示,A、B分别为竖直放置的圆轨道的最低点和最高点,已知轨道半径为0.5m,小球通过A点时速度大小为2$\sqrt{7}$m/s,则该小球通过最高点B的速度值可能是( )
如图所示,A、B分别为竖直放置的圆轨道的最低点和最高点,已知轨道半径为0.5m,小球通过A点时速度大小为2$\sqrt{7}$m/s,则该小球通过最高点B的速度值可能是( )
 如图所示,A、B分别为竖直放置的圆轨道的最低点和最高点,已知轨道半径为0.5m,小球通过A点时速度大小为2$\sqrt{7}$m/s,则该小球通过最高点B的速度值可能是( )
如图所示,A、B分别为竖直放置的圆轨道的最低点和最高点,已知轨道半径为0.5m,小球通过A点时速度大小为2$\sqrt{7}$m/s,则该小球通过最高点B的速度值可能是( )| A. | 2.1m/s | B. | 3.2m/s | C. | 6.2m/s | D. | 10m/s |
 某同学用如图所示的实验装置来验证“力的平行四边形定则”.弹簧测力计A悬挂于固定点P,下端用细线挂一重物M.弹簧测力计B的一端用细线系于O点,手持另一端水平向左拉,使结点O静止在某位置.分别读出弹簧测力计A和B的示数,并在贴于竖直木板的白纸上记录O点的位置和拉线的方向.然后根据力的平行四边形定则验证两弹簧测力计测出的弹力的合力大小是否等于重物M的重力.为了提高实验的可靠性,他改变拉力大小,进行了多次实验.
某同学用如图所示的实验装置来验证“力的平行四边形定则”.弹簧测力计A悬挂于固定点P,下端用细线挂一重物M.弹簧测力计B的一端用细线系于O点,手持另一端水平向左拉,使结点O静止在某位置.分别读出弹簧测力计A和B的示数,并在贴于竖直木板的白纸上记录O点的位置和拉线的方向.然后根据力的平行四边形定则验证两弹簧测力计测出的弹力的合力大小是否等于重物M的重力.为了提高实验的可靠性,他改变拉力大小,进行了多次实验.