题目内容
如图所示,一“?”形绝缘导轨竖直放置,处在水平向右的匀强电场中.左边的半圆弧与水平杆AB、CD相切于A、C两点,两水平杆的高度差为2L,杆AB、CD长度均为4L,O为AD、BC连线的交点,虚线MN、PQ的位置如图,其中AM=MP=CN=NQ=L,PB=QD=2L.虚线MN左边的导轨光滑,虚线MN右边的导轨与小球之间的动摩擦因数为μ.现把一质量为m,电荷量为-q的小球穿在杆上,自N点由静止释放后,小球刚好可到达A点.已知静电力常量为k,重力加速度为g.求:
(1)匀强电场的电场强度E的大小;
(2)小球到达半圆弧中点时,小球对半圆弧轨道的压力大小.
(3)若在O处固定一点电荷+Q,并将带电小球自D点以某速度向左瞬间推出,结果小球可沿杆运动到B点.求从D到B点过程中小球所受摩擦力的最大值.

(1)匀强电场的电场强度E的大小;
(2)小球到达半圆弧中点时,小球对半圆弧轨道的压力大小.
(3)若在O处固定一点电荷+Q,并将带电小球自D点以某速度向左瞬间推出,结果小球可沿杆运动到B点.求从D到B点过程中小球所受摩擦力的最大值.

分析:(1)小球刚好可到达A点的速度为零,对N到A运用动能定理,求出匀强电场的电场强度的大小.
(2)根据动能定理求出小球到达圆弧中点的速度,再根据径向的合力提供向心力,运用牛顿第二定律求出轨道对小球的支持力,根据牛顿第三定律求出球对轨道的压力.
(3)小球在P点的压力最大,根据竖直方向上的平衡求出支持力的大小,根据fm=μ N 求出摩擦力的最大值.
(2)根据动能定理求出小球到达圆弧中点的速度,再根据径向的合力提供向心力,运用牛顿第二定律求出轨道对小球的支持力,根据牛顿第三定律求出球对轨道的压力.
(3)小球在P点的压力最大,根据竖直方向上的平衡求出支持力的大小,根据fm=μ N 求出摩擦力的最大值.
解答:解:(1)小球由N到A过程,对小球列动能定理:
EqL-2mgL=0
E=
(2)小球在圆弧的中点时,由牛顿第二定律得:
N-Eq=m
小球由N到圆弧的中点过程中,对小球列动能定理:
Eq(2L)-mgL=
mv2
由 E=
,得
N=8mg
由牛顿第三定律可知:N=N'=8mg
(3)经分析可知,小球在P点的压力最大,则:
N=mg+K
fm=μ N
fm=μ(mg+K
)
答:(1)匀强电场的电场强度E的大小为
.
(2)小球对半圆弧轨道的压力大小为8mg.
(3)从D到B点过程中小球所受摩擦力的最大值为μ(mg+K
).
EqL-2mgL=0
E=
| 2mg |
| q |
(2)小球在圆弧的中点时,由牛顿第二定律得:
N-Eq=m
| v2 |
| L |
小球由N到圆弧的中点过程中,对小球列动能定理:
Eq(2L)-mgL=
| 1 |
| 2 |
由 E=
| 2mg |
| q |
N=8mg
由牛顿第三定律可知:N=N'=8mg
(3)经分析可知,小球在P点的压力最大,则:
N=mg+K
| L2 |
fm=μ N
fm=μ(mg+K
| L2 |
答:(1)匀强电场的电场强度E的大小为
| 2mg |
| q |
(2)小球对半圆弧轨道的压力大小为8mg.
(3)从D到B点过程中小球所受摩擦力的最大值为μ(mg+K
| L2 |
点评:本题综合运用了动能定理、牛顿第二定律,关键是理清小球的运动过程,选择合适的定律进行求解.

练习册系列答案
相关题目
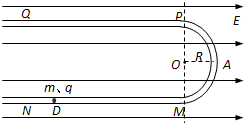 如图所示,一绝缘“?”形细管由两段相互平行的足够长的水平直管PQ、MN和一半径为R的光滑半圆管MAP组成,固定在竖直平面内,其中MN管内壁是光滑的,PQ管是粗糙的.现将一质量为m的带电小球(小球直径远小于R)放在MN管内,小球所受的电场力为重力的
如图所示,一绝缘“?”形细管由两段相互平行的足够长的水平直管PQ、MN和一半径为R的光滑半圆管MAP组成,固定在竖直平面内,其中MN管内壁是光滑的,PQ管是粗糙的.现将一质量为m的带电小球(小球直径远小于R)放在MN管内,小球所受的电场力为重力的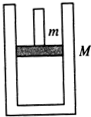 如图所示,一圆筒形汽缸静止于地面上,汽缸的质量为M,活塞(连同手柄)的质量为m,汽缸内部的横截面积为S,大气压强为p0,平衡的汽缸内的容积为V.现用手握住活塞手柄缓慢向上提.设汽缸足够长,在整个上提过程中气体的温度保持不变,不计汽缸内气体的重力与活塞与汽缸壁间的摩擦,求汽缸刚提离地面时活塞上升的距离.
如图所示,一圆筒形汽缸静止于地面上,汽缸的质量为M,活塞(连同手柄)的质量为m,汽缸内部的横截面积为S,大气压强为p0,平衡的汽缸内的容积为V.现用手握住活塞手柄缓慢向上提.设汽缸足够长,在整个上提过程中气体的温度保持不变,不计汽缸内气体的重力与活塞与汽缸壁间的摩擦,求汽缸刚提离地面时活塞上升的距离.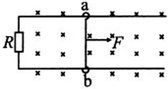 如图所示,一U形光滑导轨串有一电阻R,放置在匀强磁场中,导轨平面与磁场方向垂直.一电阻可忽略不计但有一定质量的金属杆ab跨接在导轨上,可沿导轨方向平移,现从静止开始对ab杆施以向右的恒力F,则杆在运动过程中,下列说法中正确的是( )
如图所示,一U形光滑导轨串有一电阻R,放置在匀强磁场中,导轨平面与磁场方向垂直.一电阻可忽略不计但有一定质量的金属杆ab跨接在导轨上,可沿导轨方向平移,现从静止开始对ab杆施以向右的恒力F,则杆在运动过程中,下列说法中正确的是( )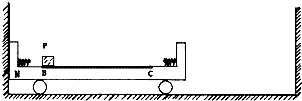
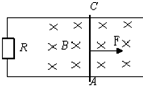 如图所示,一U形光滑金属框的可动边AC长0.1m,匀强磁场的磁感强度为0.5T.在一水平力F的作用下,AC以8m/s的速度匀速水平向右运动,电阻R为4Ω,AC的电阻为1Ω(其它电阻均不计).求:
如图所示,一U形光滑金属框的可动边AC长0.1m,匀强磁场的磁感强度为0.5T.在一水平力F的作用下,AC以8m/s的速度匀速水平向右运动,电阻R为4Ω,AC的电阻为1Ω(其它电阻均不计).求: