题目内容
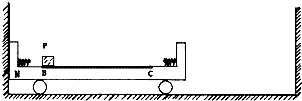
(2009?江门一模)如图所示,一凹形滑板车N放置在有两堵墙壁的光滑水平地面上,滑板内侧两端各固定一弹簧,BC段水平且表面粗糙,LBC=3.5m,其余段表面光滑,小滑块P的质量为m=1kg,滑板车N的质量M=4kg,P与BC面的动摩擦因数为μ=0.1,开始时滑板车紧靠左侧墙壁,P以V0=3m/s的初速度从B点开始向右运动,当P滑到C点时,滑板车恰好与右墙壁碰撞并立即停下来但与墙壁不粘连,P继续滑动,P可视为质点,整个过程弹簧处于弹性限度内,取g=10m/s2.问:
(1)P在BC段向右滑动到C时,P和滑板车N的速度分别多大?
(2)如果清板车与左侧墙壁的碰撞情况与右侧一样,当从N、P最终静止后,p在滑板车中的位置如何?
(1)P在BC段向右滑动到C时,P和滑板车N的速度分别多大?
(2)如果清板车与左侧墙壁的碰撞情况与右侧一样,当从N、P最终静止后,p在滑板车中的位置如何?

分析:(1)根据动量守恒定律和能量守恒定律求出P在BC段向右滑动到C时,P和滑板车N的速度.
(2)车与墙壁相碰后,P继续向右运动再反弹回到C的速度还是1m/s.根据动量守恒定律求出P和滑板车的共同速度,结合能量守恒求出P在滑板车上的相对滑行距离.判断出P的运动情况,结合动能定理求出滑板车与墙壁碰后,继续向前滑行的距离,从而得出P在滑板车中的位置.
(2)车与墙壁相碰后,P继续向右运动再反弹回到C的速度还是1m/s.根据动量守恒定律求出P和滑板车的共同速度,结合能量守恒求出P在滑板车上的相对滑行距离.判断出P的运动情况,结合动能定理求出滑板车与墙壁碰后,继续向前滑行的距离,从而得出P在滑板车中的位置.
解答:解:(1)设P从B滑至C点的速度为v1,滑板车的速度为v2,根据动量守恒定律和能量守恒定律,有:
mv0=mv1+Mv2
mv02=
mv12+
Mv22+μmgLBC
解得:v1=1m/s,v2=0.5m/s.
或v1=0.2m/s,v2=0.7m/s(不合题意舍去).
(2)车与墙壁相碰后,P继续向右运动再反弹回到C的速度还是1m/s.
设P和滑板车有共同速度为v3,根据动量守恒定律有,
mv1=mv3+Mv3
解得v3=0.2m/s
设物体相对于车滑行的距离为s1,根据动能定理有,
μmgs1=
mv12-
(m+M)v32
解得s1=0.4m.
s1<LBC,说明车与左墙壁相碰之前,车与物体达到相对静止,以后一起匀速运动直到小车与左墙壁相碰,车停止后物体做匀减速运动,设相对车滑行的距离s2,则
μmgs2=
mv32
解得s2=0.02m
所以P最后距车C端s=s1+s2=0.42m.
答:(1)P在BC段向右滑动到C时,P和滑板车N的速度分别为1m/s,0.5m/s.
(2)如果清板车与左侧墙壁的碰撞情况与右侧一样,当从N、P最终静止后,P最后距车C端0.42m.
mv0=mv1+Mv2
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得:v1=1m/s,v2=0.5m/s.
或v1=0.2m/s,v2=0.7m/s(不合题意舍去).
(2)车与墙壁相碰后,P继续向右运动再反弹回到C的速度还是1m/s.
设P和滑板车有共同速度为v3,根据动量守恒定律有,
mv1=mv3+Mv3
解得v3=0.2m/s
设物体相对于车滑行的距离为s1,根据动能定理有,
μmgs1=
| 1 |
| 2 |
| 1 |
| 2 |
解得s1=0.4m.
s1<LBC,说明车与左墙壁相碰之前,车与物体达到相对静止,以后一起匀速运动直到小车与左墙壁相碰,车停止后物体做匀减速运动,设相对车滑行的距离s2,则
μmgs2=
| 1 |
| 2 |
解得s2=0.02m
所以P最后距车C端s=s1+s2=0.42m.
答:(1)P在BC段向右滑动到C时,P和滑板车N的速度分别为1m/s,0.5m/s.
(2)如果清板车与左侧墙壁的碰撞情况与右侧一样,当从N、P最终静止后,P最后距车C端0.42m.
点评:本题综合考查了动量守恒定律、动能定理和能量守恒定律,综合性较强,对学生的要求较高,关键理清运动过程,选择合适的规律进行求解.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
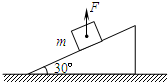 (2009?江门一模)如图所示,一个质量为m=2.0kg的物体,放在倾角为θ=30°的斜面上静止不动,若用竖直向上的力F=5.0N提物体,物体仍静止(g=10m/s2),下述结论正确的是( )
(2009?江门一模)如图所示,一个质量为m=2.0kg的物体,放在倾角为θ=30°的斜面上静止不动,若用竖直向上的力F=5.0N提物体,物体仍静止(g=10m/s2),下述结论正确的是( )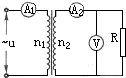 (2009?江门一模)如图所示,一理想变压器原线圈匝数n1=1100匝,副线圈匝数n2=220匝,交流电源的电压
(2009?江门一模)如图所示,一理想变压器原线圈匝数n1=1100匝,副线圈匝数n2=220匝,交流电源的电压 (2009?江门一模)2008北京奥运会取得了举世瞩目的成功,某运动员(可看作质点)参加跳板跳水比赛,起跳过程中,将运动员离开跳板时做为计时起点,其速度与时间关系图象如图所示,则( )
(2009?江门一模)2008北京奥运会取得了举世瞩目的成功,某运动员(可看作质点)参加跳板跳水比赛,起跳过程中,将运动员离开跳板时做为计时起点,其速度与时间关系图象如图所示,则( )