��Ŀ����
��ѡ��ģ��3-5��
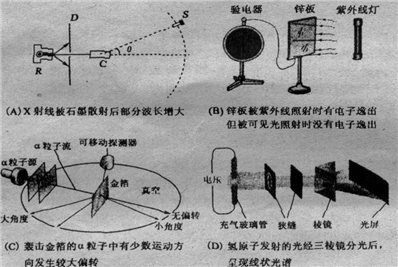
��1������ԭ�ӽṹ��ԭ�Ӻˣ�����˵������ȷ����
A�����æ�����ɢ��ʵ����Թ���ԭ�Ӻ˵İ뾶
B�����æ�����ɢ��ʵ����Թ��������ӵ��˶��뾶
C��ԭ�ӵĺ�ʽ�ṹģ�ͺܺõؽ�������ԭ�ӹ���ʵ��
D�����ڼ���̬����ԭ�ӷų����Ӻ�������˶��Ķ��ܽ�����
��2��һ������Ϊm0��ֹ�Ħؽ���˥��Ϊ������ֹ��������m�Ħн��ӣ�������ͬһƽ�����˶����˴��˶�����ļн�Ϊ120�㣬��������еĴ����ٶ�Ϊc����ÿ���н��ӵĶ���Ϊ ��
��3����ͼ5��ʾ���⻬ˮƽ����A��B��С����������M��A��ͷվ��һ����Ϊm���ˣ�������ͬһֱ���������˶���Ϊ����������ײ���˴�A��Ծ��B���ϣ�����A��ֹͣ�˶���B����÷����ٶ�v0������
����С��������ɵ�ϵͳ�ij�������С��
��Ϊ����������ײ����Ҫ������Ծ�ٶȾ���С����������B����A�����ٶȶ��
��1������ԭ�ӽṹ��ԭ�Ӻˣ�����˵������ȷ����
A�����æ�����ɢ��ʵ����Թ���ԭ�Ӻ˵İ뾶
B�����æ�����ɢ��ʵ����Թ��������ӵ��˶��뾶
C��ԭ�ӵĺ�ʽ�ṹģ�ͺܺõؽ�������ԭ�ӹ���ʵ��
D�����ڼ���̬����ԭ�ӷų����Ӻ�������˶��Ķ��ܽ�����
��2��һ������Ϊm0��ֹ�Ħؽ���˥��Ϊ������ֹ��������m�Ħн��ӣ�������ͬһƽ�����˶����˴��˶�����ļн�Ϊ120�㣬��������еĴ����ٶ�Ϊc����ÿ���н��ӵĶ���Ϊ
��3����ͼ5��ʾ���⻬ˮƽ����A��B��С����������M��A��ͷվ��һ����Ϊm���ˣ�������ͬһֱ���������˶���Ϊ����������ײ���˴�A��Ծ��B���ϣ�����A��ֹͣ�˶���B����÷����ٶ�v0������
����С��������ɵ�ϵͳ�ij�������С��
��Ϊ����������ײ����Ҫ������Ծ�ٶȾ���С����������B����A�����ٶȶ��
��������1�����ݦ�����ɢ��ʵ����Թ���ԭ�Ӻ˵İ뾶������ģ�Ϳ��Ժܺõؽ�����ԭ�ӹ���ʵ�飮ͨ������뾶�ı仯����Ͽ��������ṩ�������Ƚϵ��Ӷ��ܵı仯��
��2�����ݰ���˹̹���ܷ������ÿ���н��ӵĶ��ܣ�
��3�����ݶ����ı���ʽ�����״̬ϵͳ�ij�������С��ץס��������ǡ�ò��ᷢ����ײ�������������˾�����ͬ�ٶȣ���϶����غ㶨�����A�����ٶȣ�
��2�����ݰ���˹̹���ܷ������ÿ���н��ӵĶ��ܣ�
��3�����ݶ����ı���ʽ�����״̬ϵͳ�ij�������С��ץס��������ǡ�ò��ᷢ����ײ�������������˾�����ͬ�ٶȣ���϶����غ㶨�����A�����ٶȣ�
����⣺��1��A�����æ�����ɢ��ʵ����Թ���ԭ�Ӻ˵İ뾶�����ó����ӵİ뾶����A��ȷ��B����
C��ԭ�ӵĺ�ʽ�ṹģ������������ԭ�ӹ���ʵ�飬����ģ���ܹ��ܺý��ͣ���C����
D�����ڼ���̬����ԭ�ӷų����Ӻ��ܼ����ͣ�����뾶��С������k
=m
֪�����Ӷ�������D��ȷ��
��ѡAD��
��2�����ݰ���˹̹���ܷ��̵ã�(m0-3m)c2=3Ek
���Ek=
(m0-3m)c2��
��3�����ɶ����غ㶨�ɿ�֪��ϵͳ�ij�������С
p=��M+m��v0
��Ϊ��������ǡ�ò��ᷢ����ײ�������������˾�����ͬ�ٶȣ���Ϊv������
��M+m��v0=��2M+m��v
��� v=
�ʴ�Ϊ����1��AD ��2��
(m0-3m)c2
��3���٣�M+m��v0����
��
C��ԭ�ӵĺ�ʽ�ṹģ������������ԭ�ӹ���ʵ�飬����ģ���ܹ��ܺý��ͣ���C����
D�����ڼ���̬����ԭ�ӷų����Ӻ��ܼ����ͣ�����뾶��С������k
| e2 |
| r2 |
| v2 |
| r |
��ѡAD��
��2�����ݰ���˹̹���ܷ��̵ã�(m0-3m)c2=3Ek
���Ek=
| 1 |
| 3 |
��3�����ɶ����غ㶨�ɿ�֪��ϵͳ�ij�������С
p=��M+m��v0
��Ϊ��������ǡ�ò��ᷢ����ײ�������������˾�����ͬ�ٶȣ���Ϊv������
��M+m��v0=��2M+m��v
��� v=
| (M+m)v0 |
| 2M+m |
�ʴ�Ϊ����1��AD ��2��
| 1 |
| 3 |
��3���٣�M+m��v0����
| (M+m)v0 |
| 2M+m |
���������⿼��ѡ��3-5�е����ݣ��ѶȲ��ؼ�����Ϥ�̲ģ��μǻ�������ͻ������ɣ�

��ϰ��ϵ�д�
�����Ŀ