题目内容
18. 在现代科学实验室中,经常用磁场来控制带电粒子的运动.有这样一个仪器的内部结构简化如图:1、2两处的条形匀强磁场区边界竖直,相距为L,磁场方向相反且垂直于纸面.一质量为m、电量为-q,重力不计的粒子,粒子以速度V平行于纸面射入1区,射入时速度与水平方向夹角θ=30°.
在现代科学实验室中,经常用磁场来控制带电粒子的运动.有这样一个仪器的内部结构简化如图:1、2两处的条形匀强磁场区边界竖直,相距为L,磁场方向相反且垂直于纸面.一质量为m、电量为-q,重力不计的粒子,粒子以速度V平行于纸面射入1区,射入时速度与水平方向夹角θ=30°.(1)当1区磁感应强度大小B1=B0时,粒子从1区右边界射出时速度与竖直边界方向夹角为60°,求B0及粒子在1区运动的时间t.
(2)若2区B2=B1=B0,求粒子在1区的最高点与2区的最低点之间的高度差h.
(3)若B1=B0,为使粒子能返回1区,求B2应满足的条件.
分析 (1)画出轨迹,由几何知识求出半径,根据牛顿定律求出B0.找出轨迹的圆心角,求出时间.
(2)由几何知识求出高度差.
(3)当粒子在区域Ⅱ中轨迹恰好与右侧边界相切时,粒子恰能返回Ⅰ区.由几何知识求出半径,由牛顿定律求出B2满足的条件.
解答  解:(1)粒子在磁场中做匀速圆周运动,粒子运动轨迹如图所示:
解:(1)粒子在磁场中做匀速圆周运动,粒子运动轨迹如图所示:
由几何知识得:L=2R1sinθ,
由牛顿第二定律得:qvB0=m$\frac{{v}^{2}}{{R}_{1}}$,
解得:B0=$\frac{mv}{qL}$;
设粒子在磁场Ⅰ区中做圆周运动的周期:T=$\frac{2π{R}_{1}}{v}$=$\frac{2πL}{v}$,
粒子的运动的时间:t=$\frac{2θ}{360}$T=$\frac{2×30°}{360°}$T=$\frac{πL}{3v}$;
(2)设粒子在磁场Ⅱ区做圆周运动的半径为R2,
由牛顿第二定律得:qvB2=m$\frac{{v}^{2}}{{R}_{2}}$,
由几何知识可得:h=(R1+R2)(1-cosθ)+Ltanθ, 解得:h=(2-$\frac{2\sqrt{3}}{3}$)L;
解得:h=(2-$\frac{2\sqrt{3}}{3}$)L;
(3)粒子恰好能能返回1区时的运动轨迹如图所示:
为使粒子能再次回到Ⅰ区,应满足:
R2(1+sinθ)≤L,
由牛顿第二定律得:qvB2=m$\frac{{v}^{2}}{{R}_{2}}$,
由题意可知:B2=B1=B0,解得:B2≥$\frac{3mv}{2qL}$;
答:(1)当1区磁感应强度大小B1=B0时,粒子从1区右边界射出时速度与竖直边界方向夹角为60°,B0为$\frac{mv}{qL}$,粒子在Ⅰ区运动的时间t为$\frac{πL}{3v}$.
(2)若2区B2=B1=B0,粒子在1区的最高点与2区的最低点之间的高度差h为(2-$\frac{2\sqrt{3}}{3}$)L.
(3)若B1=B0,为使粒子能返回1区,B2应满足的条件是B2≥$\frac{3mv}{2qL}$.
点评 本题考查了粒子在磁场中的运动,分析清楚粒子运动过程、作出粒子运动轨迹是解题的关键;本题的难点在于分析临界条件,粒子恰好穿出磁场时,其轨迹往往与边界相切.

 阅读快车系列答案
阅读快车系列答案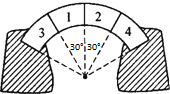 如图所示,有四块相同的坚固石块垒成弧形的石拱,每块石块的质量均为m,每块石块的两个面间所夹的圆心角均为30°,第3、第4块固定在地面上.假定石块间的摩擦力可以忽略不计,则第1与第3石块间的作用力大小为( )
如图所示,有四块相同的坚固石块垒成弧形的石拱,每块石块的质量均为m,每块石块的两个面间所夹的圆心角均为30°,第3、第4块固定在地面上.假定石块间的摩擦力可以忽略不计,则第1与第3石块间的作用力大小为( )| A. | mg | B. | $\frac{2\sqrt{3}}{3}$mg | C. | 2mg | D. | $\sqrt{3}$mg |
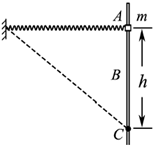 如图所示,轻质弹簧一端固定,另一端与质量为m、套在粗糙竖直固定杆A处的圆环相连,弹簧水平且处于原长.圆环从A处由静止开始下滑,经过B处的速度最大,到达C处的速度为零,AC=h.若圆环在C处获得一竖直向上的速度v,则恰好能回到A点;弹簧始终在弹性限度之内,重力加速度为g,则圆环( )
如图所示,轻质弹簧一端固定,另一端与质量为m、套在粗糙竖直固定杆A处的圆环相连,弹簧水平且处于原长.圆环从A处由静止开始下滑,经过B处的速度最大,到达C处的速度为零,AC=h.若圆环在C处获得一竖直向上的速度v,则恰好能回到A点;弹簧始终在弹性限度之内,重力加速度为g,则圆环( )| A. | 下滑过程中,加速度一直减小 | |
| B. | 下滑过程中,加速度先减小后增大 | |
| C. | 下滑过程中,克服摩擦力做功为$\frac{1}{4}$mv2 | |
| D. | 在C处,弹簧的弹性势能为$\frac{1}{4}$mv2-mgh |
| A. |  | B. |  | C. |  | D. |  |
| A. | 伽利略认为在同一地点,重的物体和轻的物体下落快慢不同 | |
| B. | 伽利略猜想运动速度与下落时间成正比,并直接用实验进行了验证 | |
| C. | 伽利略通过数学推演并用小球在斜面上运动,验证了位移与时间的平方成正比 | |
| D. | 伽利略用小球在斜面上运动“冲淡重力”,验证了运动速度与位移成正比 |
| A. | 这个电阻阻值很小,估计只有几欧姆 | |
| B. | 这个电阻阻值很大,估计有几千欧姆 | |
| C. | 如需进一步测量可换“×100”挡,调零后测量 | |
| D. | 如需进一步测量可换“×1 k”挡,调零后测量 |
 如图是主动轮 P通过皮带带动从动轮 Q的示意图,A与B、C与D分别是皮带与轮缘相互接触的点,如果皮带不打滑,当主动轮P沿顺时针方向旋转时,A、B、C、D各点所受摩擦力的方向( )
如图是主动轮 P通过皮带带动从动轮 Q的示意图,A与B、C与D分别是皮带与轮缘相互接触的点,如果皮带不打滑,当主动轮P沿顺时针方向旋转时,A、B、C、D各点所受摩擦力的方向( )| A. | 向上,向下,向下,向上 | B. | 向下,向上,向下,向上 | ||
| C. | 向下,向上,向上,向下 | D. | 向上,向下,向上,向下 |
 如图所示,木板A的质量为m=0.1kg,滑块B的质量为M=0.3kg,木板A用绳拴住,绳与斜面平行,B恰好能沿倾角为θ=37°的斜面在A木板下向下滑动.A、B间以及B与斜面间的动摩擦因数相同都为μ=0.2,sin37°=0.6,cos37°=0.8,g=10m/s2,求:
如图所示,木板A的质量为m=0.1kg,滑块B的质量为M=0.3kg,木板A用绳拴住,绳与斜面平行,B恰好能沿倾角为θ=37°的斜面在A木板下向下滑动.A、B间以及B与斜面间的动摩擦因数相同都为μ=0.2,sin37°=0.6,cos37°=0.8,g=10m/s2,求: 在《利用打点计时器测定小车作匀变速运动的加速度》的实验中:
在《利用打点计时器测定小车作匀变速运动的加速度》的实验中: