题目内容
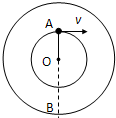 在光滑的水平面上,用一根轻绳系着一个质量为3kg的小球以10m/s的速度绕O点做匀速圆周运动,半径为4m,若运动到A点,突然将绳再放长4m,绳绷紧后小球转入到另一轨道上做匀速圆周运动.求:
在光滑的水平面上,用一根轻绳系着一个质量为3kg的小球以10m/s的速度绕O点做匀速圆周运动,半径为4m,若运动到A点,突然将绳再放长4m,绳绷紧后小球转入到另一轨道上做匀速圆周运动.求:(1)小球从放绳开始到运动到O点另一侧与AO两点共线的B点所用的时间?
(2)在B点绳子所受到的拉力.
分析:(1)小球做匀速圆周运动,突然放绳则小球以原有的速度做匀速直线运动到C,在C点处一瞬间8m绳突然拉直,沿绳方向的速度vyP突变为0,而小球将以vx做匀速圆周运动,到达B点,根据几何关系求出匀速直线运动的位移,从而得出匀速直线运动的时间,通过速度的分解求出圆周运动的速度,结合圆心角的大小求出圆周运动的时间,从而得出总时间.
(2)根据拉力提供向心力求出B点绳子的拉力大小.
(2)根据拉力提供向心力求出B点绳子的拉力大小.
解答: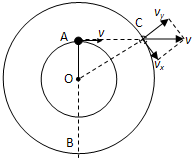 解:(1)小球做匀速圆周运动,突然放绳则小球以原有的速度做匀速直线运动到C,在C点处一瞬间8m绳突然拉直,沿绳方向的速度vy突变为0,而小球将以vx做匀速圆周运动,到达B点,
解:(1)小球做匀速圆周运动,突然放绳则小球以原有的速度做匀速直线运动到C,在C点处一瞬间8m绳突然拉直,沿绳方向的速度vy突变为0,而小球将以vx做匀速圆周运动,到达B点,
由几何关系可知:S1=AC=
=4
m
∠AOC=60°=
t1=
=
s
∠BOC=120°=
在C点,由矢量三角形可知:vx=vcos60°=
t2=
=
s
t总=t1+t2=
+
=4.04s
(2)在B点,则有:T=
=
=9.375N
答:(1)小球从放绳开始到运动到O点另一侧与AO两点共线的B点所用的时间为4.04s.
(2)在B点绳子所受到的拉力为9.375N.
 解:(1)小球做匀速圆周运动,突然放绳则小球以原有的速度做匀速直线运动到C,在C点处一瞬间8m绳突然拉直,沿绳方向的速度vy突变为0,而小球将以vx做匀速圆周运动,到达B点,
解:(1)小球做匀速圆周运动,突然放绳则小球以原有的速度做匀速直线运动到C,在C点处一瞬间8m绳突然拉直,沿绳方向的速度vy突变为0,而小球将以vx做匀速圆周运动,到达B点,由几何关系可知:S1=AC=
| OC2-OA2 |
| 3 |
∠AOC=60°=
| π |
| 3 |
t1=
| S1 |
| v |
4
| ||
| 10 |
∠BOC=120°=
| 2π |
| 3 |
在C点,由矢量三角形可知:vx=vcos60°=
| v |
| 2 |
t2=
| θR2 |
| vx |
| 2π×8 |
| 3×5 |
t总=t1+t2=
4
| ||
| 10 |
| 16π |
| 15 |
(2)在B点,则有:T=
| mvx2 |
| R2 |
| 3×25 |
| 8 |
答:(1)小球从放绳开始到运动到O点另一侧与AO两点共线的B点所用的时间为4.04s.
(2)在B点绳子所受到的拉力为9.375N.
点评:解决本题的关键知道小球从A到B过程中的运动规律,结合运动学公式进行求解,以及知道圆周运动向心力的来源.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案
相关题目
在光滑的水平面上,用F=6N的恒力,水平作用在质量为2kg的质点上,使其由静止开始运动.试比较经过5s的时间或经过5m的位移时,突然撤去拉力,得到的结论不正确是( )
| A、撤力时,前种情况的末速度大于后种情况的末速度 | B、撤力时,前种情况的末速度小于后种情况的末速度 | C、撤力前,前种情况比后种情况滑行的路程长 | D、撤力前,前种情况比后种情况滑行的时间长 |
 如图所示,在光滑的水平面上,用轻绳连接质量相等的两个物体A和B,开始弹簧处于自然伸长状态,恒力F推物体A,则从开始到弹簧第一次被压缩最短的过程中,关于物体的速度和加速度,下列说法正确的是( )
如图所示,在光滑的水平面上,用轻绳连接质量相等的两个物体A和B,开始弹簧处于自然伸长状态,恒力F推物体A,则从开始到弹簧第一次被压缩最短的过程中,关于物体的速度和加速度,下列说法正确的是( )