题目内容
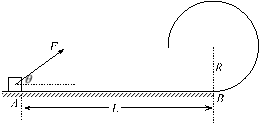
【题目】如图所示，有理想边界的两个匀强磁场，磁感应强度B＝0.5T，两边界间距s＝0.1m．一边长L＝0.2m的正方形线框abcd由粗细均匀的电阻丝围成，总电阻R＝0.4Ω。现使线框以v＝2m/s的速度从位置I匀速运动到位置II．
(1)求cd边未进入右方磁场时线框所受安培力的大小．
(2)求整个过程中线框所产生的焦耳热．
(3)在坐标图中画出整个过程中线框a、b两点的电势差Uab随时间t变化的图线．
【答案】(1)F＝5×10－2N (2)0.01J (3)如图所示: 
【解析】（1）cd边未进入右方磁场时线框时，ab边切割产生感应电动势，大小为
；
由闭合电路欧姆定律得感应电流大小为：
，
ab边受到的安培力大小为
；
（2）设克服安培力做得功为
，由功能关系得：整个过程中线框所产生的焦耳热
；
（3）cd边w未进入磁场，ab两端电势差
，由楞次定律判断出感应电流方向沿顺时针方向，则a的电势高于b的电势，
为正；cd边进入磁场后，线框中虽然感应电流为零，但ab两端仍有电势差，由右手定则判断可知，a的电势高于b的电势，为正，所以
；ab边穿出磁场后，只有cd边切割磁感线，由右手定则知，a点的电势高于b的电势，
．
整个过程中线框a、b两点的电势差随时间t变化的图线如图所示：
【题型】解答题
【结束】
22
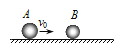
【题目】如图所示，水平传送带上A、B两端点间距L＝4m，半径R＝1m的光滑半圆形轨道固于竖直平面内，下端与传送带B相切。传送带以v0＝4m/s的速度沿图示方向匀速运动，质量m＝lkg的小滑块由静止放到传送带的A端，经一段时间运动到B端，滑块与传送带间的动摩擦因数μ＝0.5，取g＝10m/s2。
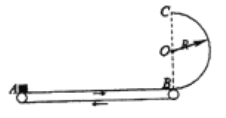
(1)求滑块到达B端的速度；
(2)求滑块由A运动到B的过程中，滑块与传送带间摩擦产生的热量；
(3)仅改变传送带的速度，其他条件不变，计算说明滑块能否通过圆轨道最高点C。
【答案】(1)vB=4m/s (2)Q＝8J (3)不能通过最高点
【解析】试题分析：⑴滑块开始时在传送带上先向右做加速运动，若传送带足够长，设当滑块速度v＝v0时已运动距离为x，根据动能定理有：μmgx＝
－0
解得：x＝1.6m＜L， 所以滑块将以速度v＝v0＝4m/s做匀速运动至B端
⑵设滑块与传送带发生相对运动的时间为t，则：v0＝μgt
皮带通过的位移为：x′＝v0t
滑块与传送带之间相对滑动的距离为：Δx＝x′－x
滑块与传送带之间产生的热量为：Q＝μmgΔx
联立以上各式解得：Q＝8J
⑶设滑块通过最高点C的最小速度为vC，经过C点时，根据向心力公式和牛顿第二定律有：mg＝
在滑块从B运动到C的过程中，根据动能定理有：－2mgR＝
－
解得要使滑块能通过圆轨道最高点C时经过B的速度最小为：vB＝
m/s
若仅改变传送带的速度，其他条件不变，使得滑块一直做匀加速直线运动至B的速度为最大速度，设为vm，根据动能定理有：μmgL＝
－0
解得：vm＝
m/s＜vB＝
m/s，所以仅改变传送带的速度，滑块不能通过圆轨道最高点
