题目内容
 (2011?浙江一模)如图,直线MN上方有平行于纸面且与MN成45°的有界匀强电场,电场强度大小为E;MN下方为方向垂直于纸面向里的有界匀强磁场,磁感应强度大小未知.今从MN上的O点向磁场中射入一个速度大小为v、方向与MN成45°角的带正电粒子,该粒子在磁场中运动时的轨道半径为R.若该粒子从O点进入磁场后第三次经过直线MN后又恰好通过O点.不计粒子的重力.求:
(2011?浙江一模)如图,直线MN上方有平行于纸面且与MN成45°的有界匀强电场,电场强度大小为E;MN下方为方向垂直于纸面向里的有界匀强磁场,磁感应强度大小未知.今从MN上的O点向磁场中射入一个速度大小为v、方向与MN成45°角的带正电粒子,该粒子在磁场中运动时的轨道半径为R.若该粒子从O点进入磁场后第三次经过直线MN后又恰好通过O点.不计粒子的重力.求:(1)粒子第三次经过直线MN时的位置;
(2)磁感应强度大小;
(3)粒子从O点出发到再次回到O点所需的时间.
分析:粒子在磁场中受洛伦兹力作用下做一段圆弧后,进入电场中恰好做匀减速运动直到速度为零后又返回,以相同速率再次进入磁场仍在洛伦兹力作用下又做一段圆弧后,再次进入电场正好做类平抛运动.粒子在磁场中两次运动刚好完成一个周期,则粒子第三次经过直线MN时的位置,就是这两段圆弧对应弦长的两倍.
由粒子在电场中的类平抛运动,垂直电场方向位移与速度关系;沿电场方向位移与时间关系,从而借助于电场强度来求出磁感应强度大小.
由粒子在电场中的类平抛运动,垂直电场方向位移与速度关系;沿电场方向位移与时间关系,从而借助于电场强度来求出磁感应强度大小.
解答: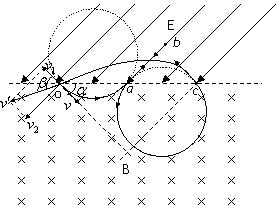 解:粒子的运动轨迹如图,先是一段半径为R的
解:粒子的运动轨迹如图,先是一段半径为R的
圆弧到a点,接着恰好逆电场线匀减速运动到b点速度为零再返回a点速度仍为v,再在磁场中运动一段
圆弧到c点,之后垂直电场线进入电场作类平抛运动.
(1)由图可知:oa=2Rcos45°=
R
因此oc=2
R 即距离O 点2
R (1)
(2)粒子在电场中运动时垂直和平行电场方向的位移都为
s⊥=s∥=ocsin45°=2R (2)
所以类平抛运动时间为
t1=
=
(3)
又 s∥=
=
(4)
再有 Bqv=m
(5)
由③④⑤⑥⑦可得
B=
(6)
(3)粒子在磁场中运动的总时间为
t2=
(7)
粒子在电场中的加速度为
a=
=
(8)
粒子在电场中做直线运动所需时间为
t3=
=
(9)
由(4)(9)(7)得粒子从出发到再到达O点所需时间
t=t1+t2+t3=
(2+π)
 解:粒子的运动轨迹如图,先是一段半径为R的
解:粒子的运动轨迹如图,先是一段半径为R的| 1 |
| 4 |
| 3 |
| 4 |
(1)由图可知:oa=2Rcos45°=
| 2 |
因此oc=2
| 2 |
| 2 |
(2)粒子在电场中运动时垂直和平行电场方向的位移都为
s⊥=s∥=ocsin45°=2R (2)
所以类平抛运动时间为
t1=
| s⊥ |
| v |
| 2R |
| v |
又 s∥=
| 1 |
| 2 |
| at | 2 3 |
| 2 3 |
再有 Bqv=m
| v2 |
| R |
由③④⑤⑥⑦可得
B=
| E |
| v |
(3)粒子在磁场中运动的总时间为
t2=
| 2πR |
| v |
粒子在电场中的加速度为
a=
| qE |
| m |
| v2 |
| R |
粒子在电场中做直线运动所需时间为
t3=
| 2v |
| a |
| 2R |
| v |
由(4)(9)(7)得粒子从出发到再到达O点所需时间
t=t1+t2+t3=
| 2R |
| v |
点评:本题考查带电粒子在电场、磁场中两运动模型:匀速圆周运动与类平抛运动,及相关的综合分析能力,以及空间想像的能力,应用数学知识解决物理问题的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2011?浙江一模)如图所示,一平行板电容器水平放置,板间距离为d,上极板开有一小孔,质量均为m,带电荷量均为+q的两个带电小球(视为质点),其间用长为L的绝缘轻杆相连,处于竖直状态,已知d=2L,今使下端小球恰好位于小孔中,由静止释放,让两球竖直下落.当下端的小球到达下极板时,速度刚好为零.试求:
(2011?浙江一模)如图所示,一平行板电容器水平放置,板间距离为d,上极板开有一小孔,质量均为m,带电荷量均为+q的两个带电小球(视为质点),其间用长为L的绝缘轻杆相连,处于竖直状态,已知d=2L,今使下端小球恰好位于小孔中,由静止释放,让两球竖直下落.当下端的小球到达下极板时,速度刚好为零.试求: (2011?浙江一模)如图所示,斜面上固定有一与斜面垂直的挡板,另有一截面为
(2011?浙江一模)如图所示,斜面上固定有一与斜面垂直的挡板,另有一截面为