题目内容

如图9-17所示，把一个带负电荷q的小球用细线悬挂在两块面积很大的竖直平行板间的O点.小球质量m=2 g，悬线长L=6 cm，两板间距离d=8 cm.当两板间加上U=2×103 V的电压时，小球自悬线水平的B点由静止开始向下运动.到达O点正下方的A点时的速度刚好为零，以后一直在A、B间来回摆动.取g=10 m/s2.求：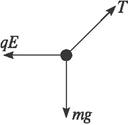

图9-17

（1）小球所带的电荷量；

（2）摆动过程中小球的最大速度.

 

解析：（1）小球受力如图.由B运动至A的过程中，T为变力，小球做变加速运动，运用动能定理解.

mg·L-qE·L=0                                                               ①

又E=                                                                     ②

由①和②解得

q== C=8×10-7 C.

（2）设在下落角为α的C点处小球速度达最大值v，如下图所示.因在小球运动过程中，张力为变力，但此张力对小球所做的功恒等于零，故采用动能定理时可不考虑张力.

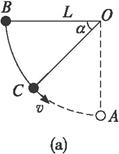
对小球自B至C的过程运用动能定理，有

mgLsinα-qEL(1-cosα)=mv2                                                  ③

mgsinα+qEcosα=mv2+qE                                                  ④

当mv2/2达极大值时，左式也达极大值，此时相应的α的数值可这样求出：作△RST，如图所示，则有

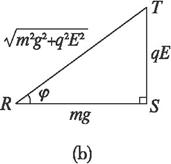
mg=m2g2+q2E2cosφ

qE=sinφ

代入④式，则其左式变为

(sinαcosφ+cosαsinφ)=sin(α+φ)

当α+φ=90°时，

mvM2=-qE

vM=.

答案：（1）8×10-7 C

（2）


练习册系列答案
相关题目
为研究静电除尘，有人设计了一个盒状容器，容器侧面是绝缘的透明有机玻璃，它的上下底面是面积A=0.04 m2的金属板，间距L=0.05 m，当连接U=2 500 V的高压电源正负两极时，能在两金属板间产生一个匀强电场，如图13-9-13所示.现把一定量均匀分布的烟尘颗粒密闭在容器内，每1 m3有烟尘颗粒1013个，假设这些颗粒都处于静止状态，每个颗粒电荷量为q=+1.0×10-17 C,质量为m=2.0×10-15 kg，不考虑烟尘颗粒之间的相互作用和空气阻力，并忽略烟尘颗粒所受重力.求合上电键后：

 图13-9-13

（1）经过多长时间烟尘颗粒可以被全部吸附？

（2）除尘过程中电场对烟尘颗粒共做了多少功？

（3）经过多长时间容器中烟尘颗粒的总动能达到最大？
如图9-3-17所示，把一个平行板电容器接在电压U=10 V的电源上，平行板电容器板间距离为d.先合上开关K，将一块厚为的金属板插入平行板电容器中央，再打开开关K，抽出金属板.此时电容器两极间电势差为_____________.

图9-3-17

第八部分 静电场

第一讲 基本知识介绍

在奥赛考纲中，静电学知识点数目不算多，总数和高考考纲基本相同，但在个别知识点上，奥赛的要求显然更加深化了：如非匀强电场中电势的计算、电容器的连接和静电能计算、电介质的极化等。在处理物理问题的方法上，对无限分割和叠加原理提出了更高的要求。

如果把静电场的问题分为两部分，那就是电场本身的问题、和对场中带电体的研究，高考考纲比较注重第二部分中带电粒子的运动问题，而奥赛考纲更注重第一部分和第二部分中的静态问题。也就是说，奥赛关注的是电场中更本质的内容，关注的是纵向的深化和而非横向的综合。

一、电场强度

1、实验定律

a、库仑定律

内容；

条件：⑴点电荷，⑵真空，⑶点电荷静止或相对静止。事实上，条件⑴和⑵均不能视为对库仑定律的限制，因为叠加原理可以将点电荷之间的静电力应用到一般带电体，非真空介质可以通过介电常数将k进行修正（如果介质分布是均匀和“充分宽广”的，一般认为k′= k /εr）。只有条件⑶，它才是静电学的基本前提和出发点（但这一点又是常常被忽视和被不恰当地“综合应用”的）。

b、电荷守恒定律

c、叠加原理

2、电场强度

a、电场强度的定义

电场的概念；试探电荷（检验电荷）；定义意味着一种适用于任何电场的对电场的检测手段；电场线是抽象而直观地描述电场有效工具（电场线的基本属性）。

b、不同电场中场强的计算

决定电场强弱的因素有两个：场源（带电量和带电体的形状）和空间位置。这可以从不同电场的场强决定式看出——

⑴点电荷：E = k

结合点电荷的场强和叠加原理，我们可以求出任何电场的场强，如——

⑵均匀带电环，垂直环面轴线上的某点P：E = ，其中r和R的意义见图7-1。

⑶均匀带电球壳

内部：E内 = 0

外部：E外 = k ，其中r指考察点到球心的距离

如果球壳是有厚度的的（内径R1 、外径R2），在壳体中（R1＜r＜R2）：

E =  ，其中ρ为电荷体密度。这个式子的物理意义可以参照万有引力定律当中（条件部分）的“剥皮法则”理解〔即为图7-2中虚线以内部分的总电量…〕。

⑷无限长均匀带电直线（电荷线密度为λ）：E = 

⑸无限大均匀带电平面（电荷面密度为σ）：E = 2πkσ

二、电势

1、电势：把一电荷从P点移到参考点P0时电场力所做的功W与该电荷电量q的比值，即

U = 

参考点即电势为零的点，通常取无穷远或大地为参考点。

和场强一样，电势是属于场本身的物理量。W则为电荷的电势能。

2、典型电场的电势

a、点电荷

以无穷远为参考点，U = k

b、均匀带电球壳

以无穷远为参考点，U外 = k ，U内 = k

3、电势的叠加

由于电势的是标量，所以电势的叠加服从代数加法。很显然，有了点电荷电势的表达式和叠加原理，我们可以求出任何电场的电势分布。

4、电场力对电荷做功

WAB = q（UA － UB）= qUAB 

三、静电场中的导体

静电感应→静电平衡（狭义和广义）→静电屏蔽

1、静电平衡的特征可以总结为以下三层含义——

a、导体内部的合场强为零；表面的合场强不为零且一般各处不等，表面的合场强方向总是垂直导体表面。

b、导体是等势体，表面是等势面。

c、导体内部没有净电荷；孤立导体的净电荷在表面的分布情况取决于导体表面的曲率。

2、静电屏蔽

导体壳（网罩）不接地时，可以实现外部对内部的屏蔽，但不能实现内部对外部的屏蔽；导体壳（网罩）接地后，既可实现外部对内部的屏蔽，也可实现内部对外部的屏蔽。

四、电容

1、电容器

孤立导体电容器→一般电容器

2、电容

a、定义式 C = 

b、决定式。决定电容器电容的因素是：导体的形状和位置关系、绝缘介质的种类，所以不同电容器有不同的电容

⑴平行板电容器 C =  =  ，其中ε为绝对介电常数（真空中ε0 =  ，其它介质中ε= ），εr则为相对介电常数，εr =  。

⑵柱形电容器：C = 

⑶球形电容器：C = 

3、电容器的连接

a、串联  = +++ … +

b、并联 C = C1 + C2 + C3 + … + Cn 

4、电容器的能量

用图7-3表征电容器的充电过程，“搬运”电荷做功W就是图中阴影的面积，这也就是电容器的储能E ，所以

E = q0U0 = C = 

电场的能量。电容器储存的能量究竟是属于电荷还是属于电场？正确答案是后者，因此，我们可以将电容器的能量用场强E表示。

对平行板电容器 E总 = E2 

认为电场能均匀分布在电场中，则单位体积的电场储能 w = E2 。而且，这以结论适用于非匀强电场。

五、电介质的极化

1、电介质的极化

a、电介质分为两类：无极分子和有极分子，前者是指在没有外电场时每个分子的正、负电荷“重心”彼此重合（如气态的H2 、O2 、N2和CO2），后者则反之（如气态的H2O 、SO2和液态的水硝基笨）

b、电介质的极化：当介质中存在外电场时，无极分子会变为有极分子，有极分子会由原来的杂乱排列变成规则排列，如图7-4所示。

2、束缚电荷、自由电荷、极化电荷与宏观过剩电荷

a、束缚电荷与自由电荷：在图7-4中，电介质左右两端分别显现负电和正电，但这些电荷并不能自由移动，因此称为束缚电荷，除了电介质，导体中的原子核和内层电子也是束缚电荷；反之，能够自由移动的电荷称为自由电荷。事实上，导体中存在束缚电荷与自由电荷，绝缘体中也存在束缚电荷和自由电荷，只是它们的比例差异较大而已。

b、极化电荷是更严格意义上的束缚电荷，就是指图7-4中电介质两端显现的电荷。而宏观过剩电荷是相对极化电荷来说的，它是指可以自由移动的净电荷。宏观过剩电荷与极化电荷的重要区别是：前者能够用来冲放电，也能用仪表测量，但后者却不能。

第二讲 重要模型与专题

一、场强和电场力

【物理情形1】试证明：均匀带电球壳内部任意一点的场强均为零。

【模型分析】这是一个叠加原理应用的基本事例。

如图7-5所示，在球壳内取一点P ，以P为顶点做两个对顶的、顶角很小的锥体，锥体与球面相交得到球面上的两个面元ΔS1和ΔS2 ，设球面的电荷面密度为σ，则这两个面元在P点激发的场强分别为

ΔE1 = k

ΔE2 = k

为了弄清ΔE1和ΔE2的大小关系，引进锥体顶部的立体角ΔΩ ，显然

 = ΔΩ = 

所以 ΔE1 = k ，ΔE2 = k ，即：ΔE1 = ΔE2 ，而它们的方向是相反的，故在P点激发的合场强为零。

同理，其它各个相对的面元ΔS3和ΔS4 、ΔS5和ΔS6 … 激发的合场强均为零。原命题得证。

【模型变换】半径为R的均匀带电球面，电荷的面密度为σ，试求球心处的电场强度。

【解析】如图7-6所示，在球面上的P处取一极小的面元ΔS ，它在球心O点激发的场强大小为

ΔE = k ，方向由P指向O点。

无穷多个这样的面元激发的场强大小和ΔS激发的完全相同，但方向各不相同，它们矢量合成的效果怎样呢？这里我们要大胆地预见——由于由于在x方向、y方向上的对称性，Σ = Σ = 0 ，最后的ΣE = ΣEz ，所以先求

ΔEz = ΔEcosθ= k ，而且ΔScosθ为面元在xoy平面的投影，设为ΔS′

所以 ΣEz = ΣΔS′

而 ΣΔS′= πR2 

【答案】E = kπσ ，方向垂直边界线所在的平面。

〖学员思考〗如果这个半球面在yoz平面的两边均匀带有异种电荷，面密度仍为σ，那么，球心处的场强又是多少？

〖推荐解法〗将半球面看成4个球面，每个球面在x、y、z三个方向上分量均为 kπσ，能够对称抵消的将是y、z两个方向上的分量，因此ΣE = ΣEx …

〖答案〗大小为kπσ，方向沿x轴方向（由带正电的一方指向带负电的一方）。

【物理情形2】有一个均匀的带电球体，球心在O点，半径为R ，电荷体密度为ρ ，球体内有一个球形空腔，空腔球心在O′点，半径为R′，= a ，如图7-7所示，试求空腔中各点的场强。

【模型分析】这里涉及两个知识的应用：一是均匀带电球体的场强定式（它也是来自叠加原理，这里具体用到的是球体内部的结论，即“剥皮法则”），二是填补法。

将球体和空腔看成完整的带正电的大球和带负电（电荷体密度相等）的小球的集合，对于空腔中任意一点P ，设 = r1 ， = r2 ，则大球激发的场强为

E1 = k = kρπr1 ，方向由O指向P

“小球”激发的场强为

E2 = k = kρπr2 ，方向由P指向O′

E1和E2的矢量合成遵从平行四边形法则，ΣE的方向如图。又由于矢量三角形PE1ΣE和空间位置三角形OP O′是相似的，ΣE的大小和方向就不难确定了。

【答案】恒为kρπa ，方向均沿O → O′，空腔里的电场是匀强电场。

〖学员思考〗如果在模型2中的OO′连线上O′一侧距离O为b（b＞R）的地方放一个电量为q的点电荷，它受到的电场力将为多大？

〖解说〗上面解法的按部就班应用…

〖答〗πkρq〔?〕。

二、电势、电量与电场力的功

【物理情形1】如图7-8所示，半径为R的圆环均匀带电，电荷线密度为λ，圆心在O点，过圆心跟环面垂直的轴线上有P点， = r ，以无穷远为参考点，试求P点的电势UP 。

【模型分析】这是一个电势标量叠加的简单模型。先在圆环上取一个元段ΔL ，它在P点形成的电势

ΔU = k

环共有段，各段在P点形成的电势相同，而且它们是标量叠加。

【答案】UP = 

〖思考〗如果上题中知道的是环的总电量Q ，则UP的结论为多少？如果这个总电量的分布不是均匀的，结论会改变吗？

〖答〗UP =  ；结论不会改变。

〖再思考〗将环换成半径为R的薄球壳，总电量仍为Q ，试问：（1）当电量均匀分布时，球心电势为多少？球内（包括表面）各点电势为多少？（2）当电量不均匀分布时，球心电势为多少？球内（包括表面）各点电势为多少？

〖解说〗（1）球心电势的求解从略；

球内任一点的求解参看图7-5

ΔU1 = k= k·= kσΔΩ

ΔU2 = kσΔΩ

它们代数叠加成 ΔU = ΔU1 + ΔU2 = kσΔΩ

而 r1 + r2 = 2Rcosα

所以 ΔU = 2RkσΔΩ

所有面元形成电势的叠加 ΣU = 2RkσΣΔΩ

注意：一个完整球面的ΣΔΩ = 4π（单位：球面度sr），但作为对顶的锥角，ΣΔΩ只能是2π ，所以——

ΣU = 4πRkσ= k

（2）球心电势的求解和〖思考〗相同；

球内任一点的电势求解可以从（1）问的求解过程得到结论的反证。

〖答〗（1）球心、球内任一点的电势均为k ；（2）球心电势仍为k ，但其它各点的电势将随电量的分布情况的不同而不同（内部不再是等势体，球面不再是等势面）。

【相关应用】如图7-9所示，球形导体空腔内、外壁的半径分别为R1和R2 ，带有净电量+q ，现在其内部距球心为r的地方放一个电量为+Q的点电荷，试求球心处的电势。

【解析】由于静电感应，球壳的内、外壁形成两个带电球壳。球心电势是两个球壳形成电势、点电荷形成电势的合效果。

根据静电感应的尝试，内壁的电荷量为－Q ，外壁的电荷量为+Q+q ，虽然内壁的带电是不均匀的，根据上面的结论，其在球心形成的电势仍可以应用定式，所以…

【答案】Uo = k － k + k 。

〖反馈练习〗如图7-10所示，两个极薄的同心导体球壳A和B，半径分别为RA和RB ，现让A壳接地，而在B壳的外部距球心d的地方放一个电量为+q的点电荷。试求：（1）A球壳的感应电荷量；（2）外球壳的电势。

〖解说〗这是一个更为复杂的静电感应情形，B壳将形成图示的感应电荷分布（但没有净电量），A壳的情形未画出（有净电量），它们的感应电荷分布都是不均匀的。

此外，我们还要用到一个重要的常识：接地导体（A壳）的电势为零。但值得注意的是，这里的“为零”是一个合效果，它是点电荷q 、A壳、B壳（带同样电荷时）单独存在时在A中形成的的电势的代数和，所以，当我们以球心O点为对象，有

UO = k + k + k = 0

QB应指B球壳上的净电荷量，故 QB = 0

所以 QA = －q

☆学员讨论：A壳的各处电势均为零，我们的方程能不能针对A壳表面上的某点去列？（答：不能，非均匀带电球壳的球心以外的点不能应用定式！）

基于刚才的讨论，求B的电势时也只能求B的球心的电势（独立的B壳是等势体，球心电势即为所求）——

UB = k + k

〖答〗（1）QA = －q ；（2）UB = k(1－) 。

【物理情形2】图7-11中，三根实线表示三根首尾相连的等长绝缘细棒，每根棒上的电荷分布情况与绝缘棒都换成导体棒时完全相同。点A是Δabc的中心，点B则与A相对bc棒对称，且已测得它们的电势分别为UA和UB 。试问：若将ab棒取走，A、B两点的电势将变为多少？

【模型分析】由于细棒上的电荷分布既不均匀、三根细棒也没有构成环形，故前面的定式不能直接应用。若用元段分割→叠加，也具有相当的困难。所以这里介绍另一种求电势的方法。

每根细棒的电荷分布虽然复杂，但相对各自的中点必然是对称的，而且三根棒的总电量、分布情况彼此必然相同。这就意味着：①三棒对A点的电势贡献都相同（可设为U1）；②ab棒、ac棒对B点的电势贡献相同（可设为U2）；③bc棒对A、B两点的贡献相同（为U1）。

所以，取走ab前  3U1 = UA

                 2U2 + U1 = UB

取走ab后，因三棒是绝缘体，电荷分布不变，故电势贡献不变，所以

  UA′= 2U1

                 UB′= U1 + U2

【答案】UA′= UA ；UB′= UA + UB 。

〖模型变换〗正四面体盒子由彼此绝缘的四块导体板构成，各导体板带电且电势分别为U1 、U2 、U3和U4 ，则盒子中心点O的电势U等于多少？

〖解说〗此处的四块板子虽然位置相对O点具有对称性，但电量各不相同，因此对O点的电势贡献也不相同，所以应该想一点办法——

我们用“填补法”将电量不对称的情形加以改观：先将每一块导体板复制三块，作成一个正四面体盒子，然后将这四个盒子位置重合地放置——构成一个有四层壁的新盒子。在这个新盒子中，每个壁的电量将是完全相同的（为原来四块板的电量之和）、电势也完全相同（为U1 + U2 + U3 + U4），新盒子表面就构成了一个等势面、整个盒子也是一个等势体，故新盒子的中心电势为

U′= U1 + U2 + U3 + U4 

最后回到原来的单层盒子，中心电势必为 U =  U′

〖答〗U = （U1 + U2 + U3 + U4）。

☆学员讨论：刚才的这种解题思想是否适用于“物理情形2”？（答：不行，因为三角形各边上电势虽然相等，但中点的电势和边上的并不相等。）

〖反馈练习〗电荷q均匀分布在半球面ACB上，球面半径为R ，CD为通过半球顶点C和球心O的轴线，如图7-12所示。P、Q为CD轴线上相对O点对称的两点，已知P点的电势为UP ，试求Q点的电势UQ 。

〖解说〗这又是一个填补法的应用。将半球面补成完整球面，并令右边内、外层均匀地带上电量为q的电荷，如图7-12所示。

从电量的角度看，右半球面可以看作不存在，故这时P、Q的电势不会有任何改变。

而换一个角度看，P、Q的电势可以看成是两者的叠加：①带电量为2q的完整球面；②带电量为－q的半球面。

考查P点，UP = k + U半球面

其中 U半球面显然和为填补时Q点的电势大小相等、符号相反，即 U半球面= －UQ 

以上的两个关系已经足以解题了。

〖答〗UQ = k － UP 。

【物理情形3】如图7-13所示，A、B两点相距2L ，圆弧是以B为圆心、L为半径的半圆。A处放有电量为q的电荷，B处放有电量为－q的点电荷。试问：（1）将单位正电荷从O点沿移到D点，电场力对它做了多少功？（2）将单位负电荷从D点沿AB的延长线移到无穷远处去，电场力对它做多少功？

【模型分析】电势叠加和关系WAB = q（UA － UB）= qUAB的基本应用。

UO = k + k = 0

UD = k + k = －

U∞ = 0

再用功与电势的关系即可。

【答案】（1）；（2）。 

【相关应用】在不计重力空间，有A、B两个带电小球，电量分别为q1和q2 ，质量分别为m1和m2 ，被固定在相距L的两点。试问：（1）若解除A球的固定，它能获得的最大动能是多少？（2）若同时解除两球的固定，它们各自的获得的最大动能是多少？（3）未解除固定时，这个系统的静电势能是多少？

【解说】第（1）问甚间；第（2）问在能量方面类比反冲装置的能量计算，另启用动量守恒关系；第（3）问是在前两问基础上得出的必然结论…（这里就回到了一个基本的观念斧正：势能是属于场和场中物体的系统，而非单纯属于场中物体——这在过去一直是被忽视的。在两个点电荷的环境中，我们通常说“两个点电荷的势能”是多少。）

【答】（1）k；（2）Ek1 = k ，Ek2 = k；（3）k 。

〖思考〗设三个点电荷的电量分别为q1 、q2和q3 ，两两相距为r12 、r23和r31 ，则这个点电荷系统的静电势能是多少？

〖解〗略。

〖答〗k（++）。

〖反馈应用〗如图7-14所示，三个带同种电荷的相同金属小球，每个球的质量均为m 、电量均为q ，用长度为L的三根绝缘轻绳连接着，系统放在光滑、绝缘的水平面上。现将其中的一根绳子剪断，三个球将开始运动起来，试求中间这个小球的最大速度。

〖解〗设剪断的是1、3之间的绳子，动力学分析易知，2球获得最大动能时，1、2之间的绳子与2、3之间的绳子刚好应该在一条直线上。而且由动量守恒知，三球不可能有沿绳子方向的速度。设2球的速度为v ，1球和3球的速度为v′，则

动量关系 mv + 2m v′= 0

能量关系 3k = 2 k + k + mv2 + 2m

解以上两式即可的v值。

〖答〗v = q 。

三、电场中的导体和电介质

【物理情形】两块平行放置的很大的金属薄板A和B，面积都是S ，间距为d（d远小于金属板的线度），已知A板带净电量+Q1 ，B板带尽电量+Q2 ，且Q2＜Q1 ，试求：（1）两板内外表面的电量分别是多少；（2）空间各处的场强；（3）两板间的电势差。

【模型分析】由于静电感应，A、B两板的四个平面的电量将呈现一定规律的分布（金属板虽然很薄，但内部合场强为零的结论还是存在的）；这里应注意金属板“很大”的前提条件，它事实上是指物理无穷大，因此，可以应用无限大平板的场强定式。

为方便解题，做图7-15，忽略边缘效应，四个面的电荷分布应是均匀的，设四个面的电荷面密度分别为σ1 、σ2 、σ3和σ4 ，显然

（σ1 + σ2）S = Q1 

（σ3 + σ4）S = Q2 

A板内部空间场强为零，有 2πk（σ1 ? σ2 ? σ3 ? σ4）= 0

A板内部空间场强为零，有 2πk（σ1 + σ2 + σ3 ? σ4）= 0

解以上四式易得 σ1 = σ4 = 

               σ2 = ?σ3 = 

有了四个面的电荷密度，Ⅰ、Ⅱ、Ⅲ空间的场强就好求了〔如EⅡ =2πk（σ1 + σ2 ? σ3 ? σ4）= 2πk〕。

最后，UAB = EⅡd

【答案】（1）A板外侧电量、A板内侧电量，B板内侧电量?、B板外侧电量；（2）A板外侧空间场强2πk，方向垂直A板向外，A、B板之间空间场强2πk，方向由A垂直指向B，B板外侧空间场强2πk，方向垂直B板向外；（3）A、B两板的电势差为2πkd，A板电势高。

〖学员思考〗如果两板带等量异号的净电荷，两板的外侧空间场强等于多少？（答：为零。）

〖学员讨论〗（原模型中）作为一个电容器，它的“电量”是多少（答：）？如果在板间充满相对介电常数为εr的电介质，是否会影响四个面的电荷分布（答：不会）？是否会影响三个空间的场强（答：只会影响Ⅱ空间的场强）？

〖学员讨论〗（原模型中）我们是否可以求出A、B两板之间的静电力？〔答：可以；以A为对象，外侧受力·（方向相左），内侧受力·（方向向右），它们合成即可，结论为F = Q1Q2 ，排斥力。〕

【模型变换】如图7-16所示，一平行板电容器，极板面积为S ，其上半部为真空，而下半部充满相对介电常数为εr的均匀电介质，当两极板分别带上+Q和?Q的电量后，试求：（1）板上自由电荷的分布；（2）两板之间的场强；（3）介质表面的极化电荷。

【解说】电介质的充入虽然不能改变内表面的电量总数，但由于改变了场强，故对电荷的分布情况肯定有影响。设真空部分电量为Q1 ，介质部分电量为Q2 ，显然有

Q1 + Q2 = Q

两板分别为等势体，将电容器看成上下两个电容器的并联，必有

U1 = U2 即  =  ，即  = 

解以上两式即可得Q1和Q2 。

场强可以根据E = 关系求解，比较常规（上下部分的场强相等）。

上下部分的电量是不等的，但场强居然相等，这怎么解释？从公式的角度看，E = 2πkσ（单面平板），当k 、σ同时改变，可以保持E不变，但这是一种结论所展示的表象。从内在的角度看，k的改变正是由于极化电荷的出现所致，也就是说，极化电荷的存在相当于在真空中形成了一个新的电场，正是这个电场与自由电荷（在真空中）形成的电场叠加成为E2 ，所以

E2 = 4πk（σ ? σ′）= 4πk（ ? ）

请注意：①这里的σ′和Q′是指极化电荷的面密度和总量；② E = 4πkσ的关系是由两个带电面叠加的合效果。

【答案】（1）真空部分的电量为Q ，介质部分的电量为Q ；（2）整个空间的场强均为 ；（3）Q 。

〖思考应用〗一个带电量为Q的金属小球，周围充满相对介电常数为εr的均匀电介质，试求与与导体表面接触的介质表面的极化电荷量。

〖解〗略。

〖答〗Q′= Q 。

四、电容器的相关计算

【物理情形1】由许多个电容为C的电容器组成一个如图7-17所示的多级网络，试问：（1）在最后一级的右边并联一个多大电容C′，可使整个网络的A、B两端电容也为C′？（2）不接C′，但无限地增加网络的级数，整个网络A、B两端的总电容是多少？

【模型分析】这是一个练习电容电路简化基本事例。

第（1）问中，未给出具体级数，一般结论应适用特殊情形：令级数为1 ，于是

 +  =  解C′即可。

第（2）问中，因为“无限”，所以“无限加一级后仍为无限”，不难得出方程

 +  = 

【答案】（1）C ；（2）C 。

【相关模型】在图7-18所示的电路中，已知C1 = C2 = C3 = C9 = 1μF ，C4 = C5 = C6 = C7 = 2μF ，C8 = C10 = 3μF ，试求A、B之间的等效电容。

【解说】对于既非串联也非并联的电路，需要用到一种“Δ→Y型变换”，参见图7-19，根据三个端点之间的电容等效，容易得出定式——

Δ→Y型：Ca = 

          Cb = 

          Cc = 

Y→Δ型：C1 = 

         C2 = 

         C3 = 

有了这样的定式后，我们便可以进行如图7-20所示的四步电路简化（为了方便，电容不宜引进新的符号表达，而是直接将变换后的量值标示在图中）——

【答】约2.23μF 。

【物理情形2】如图7-21所示的电路中，三个电容器完全相同，电源电动势ε1 = 3.0V ，ε2 = 4.5V，开关K1和K2接通前电容器均未带电，试求K1和K2接通后三个电容器的电压Uao 、Ubo和Uco各为多少。

【解说】这是一个考查电容器电路的基本习题，解题的关键是要抓与o相连的三块极板（俗称“孤岛”）的总电量为零。

电量关系：++= 0

电势关系：ε1 = Uao + Uob = Uao ? Ubo 

          ε2 = Ubo + Uoc = Ubo ? Uco 

解以上三式即可。

【答】Uao = 3.5V ，Ubo = 0.5V ，Uco = ?4.0V 。

【伸展应用】如图7-22所示，由n个单元组成的电容器网络，每一个单元由三个电容器连接而成，其中有两个的电容为3C ，另一个的电容为3C 。以a、b为网络的输入端，a′、b′为输出端，今在a、b间加一个恒定电压U ，而在a′b′间接一个电容为C的电容器，试求：（1）从第k单元输入端算起，后面所有电容器储存的总电能；（2）若把第一单元输出端与后面断开，再除去电源，并把它的输入端短路，则这个单元的三个电容器储存的总电能是多少？

【解说】这是一个结合网络计算和“孤岛现象”的典型事例。

（1）类似“物理情形1”的计算，可得 C总 = Ck = C

所以，从输入端算起，第k单元后的电压的经验公式为 Uk = 

再算能量储存就不难了。

（2）断开前，可以算出第一单元的三个电容器、以及后面“系统”的电量分配如图7-23中的左图所示。这时，C1的右板和C2的左板（或C2的下板和C3的右板）形成“孤岛”。此后，电容器的相互充电过程（C3类比为“电源”）满足——

电量关系：Q1′= Q3′

          Q2′+ Q3′= 

电势关系：+  = 

从以上三式解得 Q1′= Q3′=  ，Q2′=  ，这样系统的储能就可以用得出了。

【答】（1）Ek = ；（2） 。

〖学员思考〗图7-23展示的过程中，始末状态的电容器储能是否一样？（答：不一样；在相互充电的过程中，导线消耗的焦耳热已不可忽略。）

☆第七部分完☆

第一部分  力＆物体的平衡

第一讲 力的处理

一、矢量的运算

1、加法

表达： +  =  。

名词：为“和矢量”。

法则：平行四边形法则。如图1所示。

和矢量大小：c =  ，其中α为和的夹角。

和矢量方向：在、之间，和夹角β= arcsin

2、减法

表达： = － 。

名词：为“被减数矢量”，为“减数矢量”，为“差矢量”。

法则：三角形法则。如图2所示。将被减数矢量和减数矢量的起始端平移到一点，然后连接两时量末端，指向被减数时量的时量，即是差矢量。

差矢量大小：a =  ，其中θ为和的夹角。

差矢量的方向可以用正弦定理求得。

一条直线上的矢量运算是平行四边形和三角形法则的特例。

例题：已知质点做匀速率圆周运动，半径为R ，周期为T ，求它在T内和在T内的平均加速度大小。

解说：如图3所示，A到B点对应T的过程，A到C点对应T的过程。这三点的速度矢量分别设为、和。

根据加速度的定义 = 得：= ，= 

由于有两处涉及矢量减法，设两个差矢量 = － ，= － ，根据三角形法则，它们在图3中的大小、方向已绘出（的“三角形”已被拉伸成一条直线）。

本题只关心各矢量的大小，显然：

 =  =  =  ，且： = =  ， = 2= 

所以：=  =  =  ，=  =  =  。

（学生活动）观察与思考：这两个加速度是否相等，匀速率圆周运动是不是匀变速运动？

答：否；不是。

3、乘法

矢量的乘法有两种：叉乘和点乘，和代数的乘法有着质的不同。

⑴ 叉乘

表达：× = 

名词：称“矢量的叉积”，它是一个新的矢量。

叉积的大小：c = absinα，其中α为和的夹角。意义：的大小对应由和作成的平行四边形的面积。

叉积的方向：垂直和确定的平面，并由右手螺旋定则确定方向，如图4所示。

显然，×≠×，但有：×= －×

⑵ 点乘

表达：· = c

名词：c称“矢量的点积”，它不再是一个矢量，而是一个标量。

点积的大小：c = abcosα，其中α为和的夹角。

二、共点力的合成

1、平行四边形法则与矢量表达式

2、一般平行四边形的合力与分力的求法

余弦定理（或分割成RtΔ）解合力的大小

正弦定理解方向

三、力的分解

1、按效果分解

2、按需要——正交分解

第二讲 物体的平衡

一、共点力平衡

1、特征：质心无加速度。

2、条件：Σ = 0 ，或  = 0 ， = 0

例题：如图5所示，长为L 、粗细不均匀的横杆被两根轻绳水平悬挂，绳子与水平方向的夹角在图上已标示，求横杆的重心位置。

解说：直接用三力共点的知识解题，几何关系比较简单。

答案：距棒的左端L/4处。

（学生活动）思考：放在斜面上的均质长方体，按实际情况分析受力，斜面的支持力会通过长方体的重心吗？

解：将各处的支持力归纳成一个N ，则长方体受三个力（G 、f 、N）必共点，由此推知，N不可能通过长方体的重心。正确受力情形如图6所示（通常的受力图是将受力物体看成一个点，这时，N就过重心了）。

答：不会。

二、转动平衡

1、特征：物体无转动加速度。

2、条件：Σ= 0 ，或ΣM+ =ΣM- 

如果物体静止，肯定会同时满足两种平衡，因此用两种思路均可解题。

3、非共点力的合成

大小和方向：遵从一条直线矢量合成法则。

作用点：先假定一个等效作用点，然后让所有的平行力对这个作用点的和力矩为零。

第三讲 习题课

1、如图7所示，在固定的、倾角为α斜面上，有一块可以转动的夹板（β不定），夹板和斜面夹着一个质量为m的光滑均质球体，试求：β取何值时，夹板对球的弹力最小。

解说：法一，平行四边形动态处理。

对球体进行受力分析，然后对平行四边形中的矢量G和N1进行平移，使它们构成一个三角形，如图8的左图和中图所示。

由于G的大小和方向均不变，而N1的方向不可变，当β增大导致N2的方向改变时，N2的变化和N1的方向变化如图8的右图所示。

显然，随着β增大，N1单调减小，而N2的大小先减小后增大，当N2垂直N1时，N2取极小值，且N2min = Gsinα。

法二，函数法。

看图8的中间图，对这个三角形用正弦定理，有：

 =  ，即：N2 =  ，β在0到180°之间取值，N2的极值讨论是很容易的。

答案：当β= 90°时，甲板的弹力最小。

2、把一个重为G的物体用一个水平推力F压在竖直的足够高的墙壁上，F随时间t的变化规律如图9所示，则在t = 0开始物体所受的摩擦力f的变化图线是图10中的哪一个？

解说：静力学旨在解决静态问题和准静态过程的问题，但本题是一个例外。物体在竖直方向的运动先加速后减速，平衡方程不再适用。如何避开牛顿第二定律，是本题授课时的难点。

静力学的知识，本题在于区分两种摩擦的不同判据。

水平方向合力为零，得：支持力N持续增大。

物体在运动时，滑动摩擦力f = μN ，必持续增大。但物体在静止后静摩擦力f′≡ G ，与N没有关系。

对运动过程加以分析，物体必有加速和减速两个过程。据物理常识，加速时，f ＜ G ，而在减速时f ＞ G 。

答案：B 。

3、如图11所示，一个重量为G的小球套在竖直放置的、半径为R的光滑大环上，另一轻质弹簧的劲度系数为k ，自由长度为L（L＜2R），一端固定在大圆环的顶点A ，另一端与小球相连。环静止平衡时位于大环上的B点。试求弹簧与竖直方向的夹角θ。

解说：平行四边形的三个矢量总是可以平移到一个三角形中去讨论，解三角形的典型思路有三种：①分割成直角三角形（或本来就是直角三角形）；②利用正、余弦定理；③利用力学矢量三角形和某空间位置三角形相似。本题旨在贯彻第三种思路。

分析小球受力→矢量平移，如图12所示，其中F表示弹簧弹力，N表示大环的支持力。

（学生活动）思考：支持力N可不可以沿图12中的反方向？（正交分解看水平方向平衡——不可以。）

容易判断，图中的灰色矢量三角形和空间位置三角形ΔAOB是相似的，所以：

                                   ⑴

由胡克定律：F = k（- R）                ⑵

几何关系：= 2Rcosθ                     ⑶

解以上三式即可。

答案：arccos 。

（学生活动）思考：若将弹簧换成劲度系数k′较大的弹簧，其它条件不变，则弹簧弹力怎么变？环的支持力怎么变？

答：变小；不变。

（学生活动）反馈练习：光滑半球固定在水平面上，球心O的正上方有一定滑轮，一根轻绳跨过滑轮将一小球从图13所示的A位置开始缓慢拉至B位置。试判断：在此过程中，绳子的拉力T和球面支持力N怎样变化？

解：和上题完全相同。

答：T变小，N不变。

4、如图14所示，一个半径为R的非均质圆球，其重心不在球心O点，先将它置于水平地面上，平衡时球面上的A点和地面接触；再将它置于倾角为30°的粗糙斜面上，平衡时球面上的B点与斜面接触，已知A到B的圆心角也为30°。试求球体的重心C到球心O的距离。

解说：练习三力共点的应用。

根据在平面上的平衡，可知重心C在OA连线上。根据在斜面上的平衡，支持力、重力和静摩擦力共点，可以画出重心的具体位置。几何计算比较简单。

答案：R 。

（学生活动）反馈练习：静摩擦足够，将长为a 、厚为b的砖块码在倾角为θ的斜面上，最多能码多少块？

解：三力共点知识应用。

答： 。

4、两根等长的细线，一端拴在同一悬点O上，另一端各系一个小球，两球的质量分别为m1和m2 ，已知两球间存在大小相等、方向相反的斥力而使两线张开一定角度，分别为45和30°，如图15所示。则m1 : m2??为多少？

解说：本题考查正弦定理、或力矩平衡解静力学问题。

对两球进行受力分析，并进行矢量平移，如图16所示。

首先注意，图16中的灰色三角形是等腰三角形，两底角相等，设为α。

而且，两球相互作用的斥力方向相反，大小相等，可用同一字母表示，设为F 。

对左边的矢量三角形用正弦定理，有：

 =          ①

同理，对右边的矢量三角形，有： =                                ②

解①②两式即可。

答案：1 ： 。

（学生活动）思考：解本题是否还有其它的方法？

答：有——将模型看成用轻杆连成的两小球，而将O点看成转轴，两球的重力对O的力矩必然是平衡的。这种方法更直接、简便。

应用：若原题中绳长不等，而是l1 ：l2 = 3 ：2 ，其它条件不变，m1与m2的比值又将是多少？

解：此时用共点力平衡更加复杂（多一个正弦定理方程），而用力矩平衡则几乎和“思考”完全相同。

答：2 ：3 。

5、如图17所示，一个半径为R的均质金属球上固定着一根长为L的轻质细杆，细杆的左端用铰链与墙壁相连，球下边垫上一块木板后，细杆恰好水平，而木板下面是光滑的水平面。由于金属球和木板之间有摩擦（已知摩擦因素为μ），所以要将木板从球下面向右抽出时，至少需要大小为F的水平拉力。试问：现要将木板继续向左插进一些，至少需要多大的水平推力？

解说：这是一个典型的力矩平衡的例题。

以球和杆为对象，研究其对转轴O的转动平衡，设木板拉出时给球体的摩擦力为f ，支持力为N ，重力为G ，力矩平衡方程为：

f R + N（R + L）= G（R + L）           ①

球和板已相对滑动，故：f = μN        ②

解①②可得：f = 

再看木板的平衡，F = f 。

同理，木板插进去时，球体和木板之间的摩擦f′=  = F′。

答案： 。

第四讲 摩擦角及其它

一、摩擦角

1、全反力：接触面给物体的摩擦力与支持力的合力称全反力，一般用R表示，亦称接触反力。

2、摩擦角：全反力与支持力的最大夹角称摩擦角，一般用φm表示。

此时，要么物体已经滑动，必有：φm = arctgμ（μ为动摩擦因素），称动摩擦力角；要么物体达到最大运动趋势，必有：φms = arctgμs（μs为静摩擦因素），称静摩擦角。通常处理为φm = φms 。

3、引入全反力和摩擦角的意义：使分析处理物体受力时更方便、更简捷。

二、隔离法与整体法

1、隔离法：当物体对象有两个或两个以上时，有必要各个击破，逐个讲每个个体隔离开来分析处理，称隔离法。

在处理各隔离方程之间的联系时，应注意相互作用力的大小和方向关系。

2、整体法：当各个体均处于平衡状态时，我们可以不顾个体的差异而讲多个对象看成一个整体进行分析处理，称整体法。

应用整体法时应注意“系统”、“内力”和“外力”的涵义。

三、应用

1、物体放在水平面上，用与水平方向成30°的力拉物体时，物体匀速前进。若此力大小不变，改为沿水平方向拉物体，物体仍能匀速前进，求物体与水平面之间的动摩擦因素μ。

解说：这是一个能显示摩擦角解题优越性的题目。可以通过不同解法的比较让学生留下深刻印象。

法一，正交分解。（学生分析受力→列方程→得结果。）

法二，用摩擦角解题。

引进全反力R ，对物体两个平衡状态进行受力分析，再进行矢量平移，得到图18中的左图和中间图（注意：重力G是不变的，而全反力R的方向不变、F的大小不变），φm指摩擦角。

再将两图重叠成图18的右图。由于灰色的三角形是一个顶角为30°的等腰三角形，其顶角的角平分线必垂直底边……故有：φm = 15°。

最后，μ= tgφm 。

答案：0.268 。

（学生活动）思考：如果F的大小是可以选择的，那么能维持物体匀速前进的最小F值是多少？

解：见图18，右图中虚线的长度即Fmin ，所以，Fmin = Gsinφm 。

答：Gsin15°（其中G为物体的重量）。

2、如图19所示，质量m = 5kg的物体置于一粗糙斜面上，并用一平行斜面的、大小F = 30N的推力推物体，使物体能够沿斜面向上匀速运动，而斜面体始终静止。已知斜面的质量M = 10kg ，倾角为30°，重力加速度g = 10m/s2 ，求地面对斜面体的摩擦力大小。

解说：

本题旨在显示整体法的解题的优越性。

法一，隔离法。简要介绍……

法二，整体法。注意，滑块和斜面随有相对运动，但从平衡的角度看，它们是完全等价的，可以看成一个整体。

做整体的受力分析时，内力不加考虑。受力分析比较简单，列水平方向平衡方程很容易解地面摩擦力。

答案：26.0N 。

（学生活动）地面给斜面体的支持力是多少？

解：略。

答：135N 。

应用：如图20所示，一上表面粗糙的斜面体上放在光滑的水平地面上，斜面的倾角为θ。另一质量为m的滑块恰好能沿斜面匀速下滑。若用一推力F作用在滑块上，使之能沿斜面匀速上滑，且要求斜面体静止不动，就必须施加一个大小为P = 4mgsinθcosθ的水平推力作用于斜面体。使满足题意的这个F的大小和方向。

解说：这是一道难度较大的静力学题，可以动用一切可能的工具解题。

法一：隔离法。

由第一个物理情景易得，斜面于滑块的摩擦因素μ= tgθ

对第二个物理情景，分别隔离滑块和斜面体分析受力，并将F沿斜面、垂直斜面分解成Fx和Fy ，滑块与斜面之间的两对相互作用力只用两个字母表示（N表示正压力和弹力，f表示摩擦力），如图21所示。

对滑块，我们可以考查沿斜面方向和垂直斜面方向的平衡——

Fx = f + mgsinθ

Fy + mgcosθ= N

且 f = μN = Ntgθ

综合以上三式得到：

Fx = Fytgθ+ 2mgsinθ               ①

对斜面体，只看水平方向平衡就行了——

P = fcosθ+ Nsinθ

即：4mgsinθcosθ=μNcosθ+ Nsinθ

代入μ值，化简得：Fy = mgcosθ      ②

②代入①可得：Fx = 3mgsinθ

最后由F =解F的大小，由tgα= 解F的方向（设α为F和斜面的夹角）。

答案：大小为F = mg，方向和斜面夹角α= arctg()指向斜面内部。

法二：引入摩擦角和整体法观念。

仍然沿用“法一”中关于F的方向设置（见图21中的α角）。

先看整体的水平方向平衡，有：Fcos(θ- α) = P                                   ⑴

再隔离滑块，分析受力时引进全反力R和摩擦角φ，由于简化后只有三个力（R、mg和F），可以将矢量平移后构成一个三角形，如图22所示。

在图22右边的矢量三角形中，有： = =      ⑵

注意：φ= arctgμ= arctg(tgθ) = θ                                              ⑶

解⑴⑵⑶式可得F和α的值。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网