题目内容
【题目】如图1所示,两根足够长的平行金属导轨MN、PQ相距为L,导轨平面与水平面夹角为α,金属棒ab垂直于MN、PQ放置在导轨上,且始终与导轨接触良好,金属棒的质量为m.导轨处于匀强磁场中,磁场的方向垂直于导轨平面斜向上,磁感应强度大小为B.金属导轨的上端与开关S、定值电阻R1和电阻箱R2相连.不计一切摩擦,不计导轨、金属棒的电阻,重力加速度为g.现在闭合开关S,将金属棒由静止释放.
(1)判断金属棒ab中电流的方向;
(2)若电阻箱R2接入电路的阻值为0,当金属棒下降高度为h时,速度为v,求此过程中定值电阻上产生的焦耳热Q;
(3)当B=0.40T,L=0.50m,α=37°时,金属棒能达到的最大速度vm随电阻箱R2阻值的变化关系,如图2所示.取g=10m/s2 , sin37°=0.60,cos37°=0.80. 求定值电阻的阻值R1和金属棒的质量m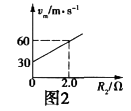
【答案】
(1)解:由右手定则,金属棒ab中的电流方向为b到a.
(2)解:由能量守恒,金属棒减小的重力势能等于增加的动能和电路中产生的焦耳热:
![]()
解得R1产生的热量: ![]()
(3)解:设最大速度为v,切割磁感线产生的感应电动势:
E=BLv
由闭合电路的欧姆定律:
![]()
从b端向a端看,金属棒受力如图:

金属棒达到最大速度时满足:
mgsinα﹣BIL=0
由以上三式得: ![]()
由图象可知:斜率为: ![]() ,纵截距为v0=30m/s,得到:
,纵截距为v0=30m/s,得到:
![]()
![]()
解得:R1=2.0Ω,m=0.1kg.
答:定值电阻的阻值R1=2.0Ω,金属棒的质量m=0.1kg.
【解析】(1)金属棒由静止释放沿导轨向下运动切割磁感线,根据右手定制判断感应电流的方向;(2)以金属棒为研究对象,根据动能定律可正确解答;(3)当金属棒的速度达到最大时,有mgsinα=BIL成立,由此写出最大速度vm和电阻R2的函数关系,根据斜率、截距的物理意义即可正确解答.
【考点精析】本题主要考查了动能定理的综合应用的相关知识点,需要掌握应用动能定理只考虑初、末状态,没有守恒条件的限制,也不受力的性质和物理过程的变化的影响.所以,凡涉及力和位移,而不涉及力的作用时间的动力学问题,都可以用动能定理分析和解答,而且一般都比用牛顿运动定律和机械能守恒定律简捷才能正确解答此题.