Question

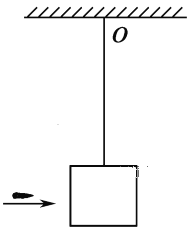
【题目】如图所示，一沙袋用无弹性轻细绳悬于O点．开始时沙袋处于静止，此后弹丸以水平速度击中沙袋后均未穿出．第一次弹丸的速度为v1，打入沙袋后二者共同摆动的最大摆角为30°.当他们第1次返回图示位置时，第2粒弹丸以水平速度v2又击中沙袋，使沙袋向右摆动且最大摆角仍为30°.若弹丸质量是沙袋质量的倍，则以下结论中正确的是(　　)

A. v1:v2＝41:42 B. v1:v2＝41:83

C. v2＝v1 D. v1:v2＝42:41

Answer 1

【答案】B

【解析】

设子弹的质量为m，沙袋质量为M=40m，取向右方向为正，第一次射入过程，根据动量守恒定律得：mv1=41mv

根据系统沙袋又返回时速度大小仍为v，但方向向左，第2粒弹丸以水平速度v2击中沙袋过程：根据动量守恒定律

mv241mv=42mv′

子弹打入沙袋后二者共同摆动的过程中，设细绳长为L，由机械能守恒得

(M+m)gL(1cos30)= (M+m)v2

得v=

可见v与系统的质量无关，故两次最大摆角均为30，故v′=v

故v1：v2=41：83，故ACD错误，B正确。

故选：B