题目内容
10.在“探究小车速度随时间变化的规律”的实验中,小车做匀加速直线运动,打点计时器接在50HZ的低压交变电源上.某同学在打出的纸带上如图1每5点取一个计数点,共取了A、B、C、D、E、F六个计数点(每相邻两个计数点间的四个点未画出).从每一个计数点处将纸带剪开分成五段(分别为a、b、c、d、e段),将这五段纸带由短到长紧靠但不重叠地粘在xoy坐标系中,如图2所示,由此可以得到一条表示v-t关系的图线,从而求出加速度的大小.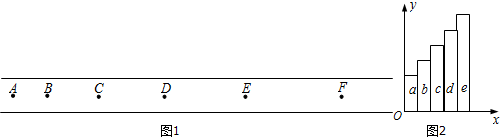
(1)从第一个计数点开始计时,为求出0.15s时刻的瞬时速度,需要测出哪一段纸带的长度?答:b;
(2)若测得a段纸带的长度为2.0cm,e段纸带的长度为10.0cm,则可求出加速度的大小为2.0m/s2.
分析 使用的方法是等效代替法解题,它们的长度分别等于x=v平均t,因为剪断的纸带所用的时间都是t=0.1s,即时间t相等,所以纸带的长度之比等于此段纸带的平均速度之比,此段纸带的平均速度等于这段纸带中间时刻的速度,根据速度时间公式求出加速度.
解答 解:(1)纸带的高度之比等于中间时刻速度之比,也就是说图中a段纸带高度代表0.05s时的瞬时速度,同理b纸带的高度代表0.15s时的瞬时速度.所以为求出0.15s时刻的瞬时速度,需要测出b段纸带的长度.
(2)若测得a段纸带的长度为2.0cm,则有:v0.05=$\frac{0.02}{0.1}m/s=0.2m/s$,
e段纸带的长度为10.0cm,v0.45=$\frac{0.10}{0.1}m/s=1.0m/s$,
则加速度为:a=$\frac{△v}{△t}=\frac{0.8}{0.4}m/{s}^{2}=2.0m/{s}^{2}$.
故答案为:(1)b;(2)2.0;
点评 纸带的长度之比等于此段纸带的平均速度之比,还等于各段纸带中间时刻的速度之比,即纸带的高度之比等于中间时刻速度之比.这种等效替代的方法减小了解题难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.电路如图所示,当滑动变阻器的触头P向上滑动时,则( )
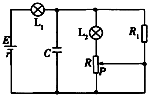

| A. | 电源的总功率变小 | B. | 电容器贮存的电量变小 | ||
| C. | 灯L1变亮 | D. | 灯L2变暗 |
1. 如图所示,一小球从距竖直弹簧一定高度静止释放,与弹簧接触后压缩弹簧到最低点(设此点小球的重力势能为0).在此过程中,小球重力势能和动能的最大值分别为Ep和Ek,弹簧弹性势能的最大值为E′p则它们之间的关系为( )
如图所示,一小球从距竖直弹簧一定高度静止释放,与弹簧接触后压缩弹簧到最低点(设此点小球的重力势能为0).在此过程中,小球重力势能和动能的最大值分别为Ep和Ek,弹簧弹性势能的最大值为E′p则它们之间的关系为( )
 如图所示,一小球从距竖直弹簧一定高度静止释放,与弹簧接触后压缩弹簧到最低点(设此点小球的重力势能为0).在此过程中,小球重力势能和动能的最大值分别为Ep和Ek,弹簧弹性势能的最大值为E′p则它们之间的关系为( )
如图所示,一小球从距竖直弹簧一定高度静止释放,与弹簧接触后压缩弹簧到最低点(设此点小球的重力势能为0).在此过程中,小球重力势能和动能的最大值分别为Ep和Ek,弹簧弹性势能的最大值为E′p则它们之间的关系为( )| A. | Ep=E′p>Ek | B. | Ep>Ek>E′p | C. | Ep=Ek+E′p | D. | Ep+Ek=E′p |
18.在平直道路上,甲汽车以速度v匀速行驶.当甲车司机发现前方距离为d处的乙汽车时,立即以大小为a1的加速度匀减速行驶,与此同时,乙车司机也发现了甲,立即从静止开始以大小为a2的加速度沿甲车运动的方向匀加速运动.则 ( )
| A. | 甲、乙两车之间的距离一定不断减小 | |
| B. | 甲、乙两车之间的距离一定不断增大 | |
| C. | 若v>$\sqrt{2{a}_{1}+{a}_{2}d}$,则两车一定不会相撞 | |
| D. | 若v<$\sqrt{2({a}_{1}+{a}_{2})d}$,则两车一定不会相撞 |
15.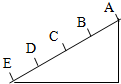 如图所示,光滑斜面AE被分成四个相等的部分,一物体由A点从静止释放,沿着斜面做匀加速直线运动,下列结论中正确的是( )
如图所示,光滑斜面AE被分成四个相等的部分,一物体由A点从静止释放,沿着斜面做匀加速直线运动,下列结论中正确的是( )
 如图所示,光滑斜面AE被分成四个相等的部分,一物体由A点从静止释放,沿着斜面做匀加速直线运动,下列结论中正确的是( )
如图所示,光滑斜面AE被分成四个相等的部分,一物体由A点从静止释放,沿着斜面做匀加速直线运动,下列结论中正确的是( )| A. | 各段的速度增加量相等 | |
| B. | 各段位移所用的时间之比为tAB:tBC:tCD:tDE=1:$\sqrt{2}$:$\sqrt{3}$:2 | |
| C. | 物体从A到E的平均速度$\overline{v}$AE=vB | |
| D. | 物体在C点的速度vC=$\sqrt{\frac{{v}_{B}^{2}+{v}_{D}^{2}}{2}}$且vC>$\frac{{v}_{B}+{v}_{D}}{2}$ |
2. 位于水平面上的物体在水平恒力F1作用下,做速度为v1的匀速运动;若作用力变为斜向下的恒力F2,物体做速度为v2的匀速运动,且F1与F2功率相同.则有( )
位于水平面上的物体在水平恒力F1作用下,做速度为v1的匀速运动;若作用力变为斜向下的恒力F2,物体做速度为v2的匀速运动,且F1与F2功率相同.则有( )
 位于水平面上的物体在水平恒力F1作用下,做速度为v1的匀速运动;若作用力变为斜向下的恒力F2,物体做速度为v2的匀速运动,且F1与F2功率相同.则有( )
位于水平面上的物体在水平恒力F1作用下,做速度为v1的匀速运动;若作用力变为斜向下的恒力F2,物体做速度为v2的匀速运动,且F1与F2功率相同.则有( )| A. | F2=F1,v1<v2 | B. | F2=F1,v1>v2 | C. | F2<F1,v1<v2 | D. | F2>F1,v1>v2 |
20.两个力的大小分别为30N和40N,则它们的合力大小可能为( )
| A. | 0N | B. | 5N | C. | 20N | D. | 80N |