题目内容
如图所示(甲),一辆汽车车厢右端放一质量为m的木箱(可视为质点),汽车车厢底板总长L=9m,汽车车厢底板距离地面的高度H=5m,木箱与汽车车厢底板间的动摩擦因数µ=0.4,最大静摩擦力等于滑动摩擦力,取g=10m/s2(计算结果保留三位有效数字).
(1)若汽车从静止开始启动,为了保证启动过程中木箱和汽车车厢底板间不发生相对滑动,求汽车的最大加速度a;
(2)若汽车由静止开始以a=6m/s2的加速度匀加速行驶,求木箱落到地面上时距离车厢左端的水平距离(木箱离开车厢后竖直方向为自由落体);
(3)若汽车从静止开始一直以(2)中加速度加速运动,为了防止木箱从车厢左端滑出,在车厢左端处安装一只长度可忽略的轻弹簧(如图乙所示),此时弹簧处于压缩状态并被锁定.每次当木箱滑至左端与弹簧发生碰撞时,弹簧都将自动解锁,并都以碰前瞬间木箱速率(相对于车)的2倍速率(相对于车)将木箱弹出,同时又将弹簧压缩并重新锁定.如此反复,通过多次碰撞最终使木箱静止于车厢内,试求木箱在车厢内滑行的总路程.
(已知:当0<A<1,n→+∞时,
 ;)
;)
【答案】分析:(1)木箱和汽车车厢底板间恰好不发生相对滑动时,静摩擦力达到最大,由牛顿第二定律求解最大加速度a.
(2)汽车由静止开始以a加速度匀加速行驶时,木箱相对于地向右做匀加速运动,当两者的位移之差L时,木箱离开汽车,由L= -
-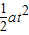 求出时间,由v=at求出木箱离开汽车时的速度大小.木箱离开车厢后做平抛运动,由高度求出时间,再由运动学公式分别求出平抛运动过程中木箱的水平位移和汽车通过的位移,由位移关系求解木箱落到地面上时距离车厢左端的水平距离.
求出时间,由v=at求出木箱离开汽车时的速度大小.木箱离开车厢后做平抛运动,由高度求出时间,再由运动学公式分别求出平抛运动过程中木箱的水平位移和汽车通过的位移,由位移关系求解木箱落到地面上时距离车厢左端的水平距离.
(3)当木箱相对于车向左滑动时相对于车的加速度大小为a相=a-a=2m/s2,设木箱滑到车厢的左端时相对车的速度为v1,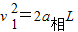 .弹簧将木箱弹出时,木箱相对于车向右滑动时,木箱相对于车厢的加速度大小为a相′=a+a=10m/s2,木箱相对于车向右做匀减速运动,设向右滑行至距离左端L1处停止,有(2v1)2=2a相′L1.可得,L1=0.8L.用同样的方法得到木箱第n次与弹簧碰撞后向右滑行的距离为Ln.即可得到木箱在车厢内滑行的总路程.
.弹簧将木箱弹出时,木箱相对于车向右滑动时,木箱相对于车厢的加速度大小为a相′=a+a=10m/s2,木箱相对于车向右做匀减速运动,设向右滑行至距离左端L1处停止,有(2v1)2=2a相′L1.可得,L1=0.8L.用同样的方法得到木箱第n次与弹簧碰撞后向右滑行的距离为Ln.即可得到木箱在车厢内滑行的总路程.
解答:解:(1)木箱和车厢恰好不发生相对滑动时,加速度最大,则由根据牛顿第二定律得
μmg=ma
解得,a=μg=4m/s2.
(2)设木箱在车厢上滑动的时间为t,则有
L=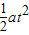 -
-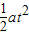
得 t=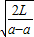 =3s
=3s
木箱离开汽车时的速度大小为v=at=12m/s,汽车此时的速度为V=at=18m/s
木箱离开车厢后做平抛运动,则有
H=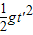
解得,t′=1s
所以s=(Vt′+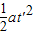 )-vt′=9m
)-vt′=9m
(3)当木箱相对于车向左滑动时相对于车的加速度大小为a相=a-a=2m/s2,
设木箱滑到车厢的左端时相对车的速度为v1.
由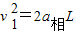 ①
①
弹簧将木箱弹出时,木箱相对于车向右滑动时,木箱相对于车厢的加速度大小为
a相′=a+a=10m/s2,木箱相对于车向右做匀减速运动,设向右滑行至距离左端L1处停止,则有
(2v1)2=2a相′L1 ②
由①②得,L1=0.8L
设第二次碰到弹簧前的速度大小为v2,则有
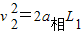 ③
③
设第二次向右滑行至距离左端L2处停止,则有
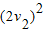 =2a相′L2 ④
=2a相′L2 ④
由③④得,L2=0.8L1=0.82L
…
根据递推规律可知,设木箱第n次与弹簧碰撞后向右滑行的距离为Ln.

故木箱在车厢内滑行的总路程为
S=L+2×0.8L+2×0.82L+…+2(0.8)nL
其中n→∞
由题意知,S=L+2 =9L=81m.
=9L=81m.
答:
(1)汽车的最大加速度a是4m/s2;
(2)木箱落到地面上时距离车厢左端的水平距离是9m.
(3)木箱在车厢内滑行的总路程是81m.
点评:本题是有相对运动的问题,运用牛顿第二定律和运动学公式解决这类问题是基本方法.第3问根据相对加速度和相对速度,求解相对位移,寻找规律,得到总路程.
(2)汽车由静止开始以a加速度匀加速行驶时,木箱相对于地向右做匀加速运动,当两者的位移之差L时,木箱离开汽车,由L=
 -
-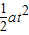 求出时间,由v=at求出木箱离开汽车时的速度大小.木箱离开车厢后做平抛运动,由高度求出时间,再由运动学公式分别求出平抛运动过程中木箱的水平位移和汽车通过的位移,由位移关系求解木箱落到地面上时距离车厢左端的水平距离.
求出时间,由v=at求出木箱离开汽车时的速度大小.木箱离开车厢后做平抛运动,由高度求出时间,再由运动学公式分别求出平抛运动过程中木箱的水平位移和汽车通过的位移,由位移关系求解木箱落到地面上时距离车厢左端的水平距离.(3)当木箱相对于车向左滑动时相对于车的加速度大小为a相=a-a=2m/s2,设木箱滑到车厢的左端时相对车的速度为v1,
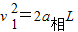 .弹簧将木箱弹出时,木箱相对于车向右滑动时,木箱相对于车厢的加速度大小为a相′=a+a=10m/s2,木箱相对于车向右做匀减速运动,设向右滑行至距离左端L1处停止,有(2v1)2=2a相′L1.可得,L1=0.8L.用同样的方法得到木箱第n次与弹簧碰撞后向右滑行的距离为Ln.即可得到木箱在车厢内滑行的总路程.
.弹簧将木箱弹出时,木箱相对于车向右滑动时,木箱相对于车厢的加速度大小为a相′=a+a=10m/s2,木箱相对于车向右做匀减速运动,设向右滑行至距离左端L1处停止,有(2v1)2=2a相′L1.可得,L1=0.8L.用同样的方法得到木箱第n次与弹簧碰撞后向右滑行的距离为Ln.即可得到木箱在车厢内滑行的总路程.解答:解:(1)木箱和车厢恰好不发生相对滑动时,加速度最大,则由根据牛顿第二定律得
μmg=ma
解得,a=μg=4m/s2.
(2)设木箱在车厢上滑动的时间为t,则有
L=
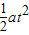 -
-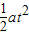
得 t=
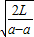 =3s
=3s木箱离开汽车时的速度大小为v=at=12m/s,汽车此时的速度为V=at=18m/s
木箱离开车厢后做平抛运动,则有
H=
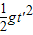
解得,t′=1s
所以s=(Vt′+
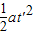 )-vt′=9m
)-vt′=9m(3)当木箱相对于车向左滑动时相对于车的加速度大小为a相=a-a=2m/s2,
设木箱滑到车厢的左端时相对车的速度为v1.
由
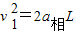 ①
①弹簧将木箱弹出时,木箱相对于车向右滑动时,木箱相对于车厢的加速度大小为
a相′=a+a=10m/s2,木箱相对于车向右做匀减速运动,设向右滑行至距离左端L1处停止,则有
(2v1)2=2a相′L1 ②
由①②得,L1=0.8L
设第二次碰到弹簧前的速度大小为v2,则有
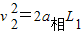 ③
③设第二次向右滑行至距离左端L2处停止,则有
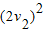 =2a相′L2 ④
=2a相′L2 ④由③④得,L2=0.8L1=0.82L
…
根据递推规律可知,设木箱第n次与弹簧碰撞后向右滑行的距离为Ln.

故木箱在车厢内滑行的总路程为
S=L+2×0.8L+2×0.82L+…+2(0.8)nL
其中n→∞
由题意知,S=L+2
 =9L=81m.
=9L=81m.答:
(1)汽车的最大加速度a是4m/s2;
(2)木箱落到地面上时距离车厢左端的水平距离是9m.
(3)木箱在车厢内滑行的总路程是81m.
点评:本题是有相对运动的问题,运用牛顿第二定律和运动学公式解决这类问题是基本方法.第3问根据相对加速度和相对速度,求解相对位移,寻找规律,得到总路程.

练习册系列答案
相关题目

 的球以相同速度v水平抛回给甲,甲接到后,再以相同速度v将此球抛给乙,这样反复进行,乙每次抛回给甲的球的质量都等于他接的球的质量的2倍,求:
的球以相同速度v水平抛回给甲,甲接到后,再以相同速度v将此球抛给乙,这样反复进行,乙每次抛回给甲的球的质量都等于他接的球的质量的2倍,求:

