题目内容
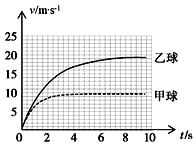
【题目】在某次火箭升空实验中,让火箭由地面竖直向上射出,以射出时做为计时起点,其速度随时间变化关系如图所示,根据图象,求:(计算结果可保留根号)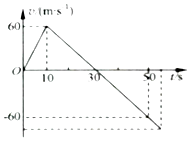
(1)该火箭在加速上升过程中的加速度大小及上升的最大高度;
(2)火箭由最大高度处至落回地面所用的时间;
(3)火箭落回地面时的速度大小.
【答案】
(1)解:由图可知,在0﹣10s内,火箭匀加速上升,则加速度为:
a= ![]() =
= ![]() =6m/s2;
=6m/s2;
火箭在0﹣30s一直上升,30s以后下落,则火箭在t=30s时,到达最高点,则火箭上升最大高度等于0﹣30s内的位移大小,为:
H= ![]() =
= ![]() =900m
=900m
答:该火箭在加速上升过程中的加速度大小是6m/s2,上升的最大高度是900m;
(2)火箭下落过程的加速度大小为 a′=| ![]() |=|
|=| ![]() |=3m/s2;
|=3m/s2;
设火箭由最大高度处至落回地面所用的时间为t′,则 H= ![]() 得
得
t′= ![]() =
= ![]() =10
=10 ![]() s
s
答:火箭由最大高度处至落回地面所用的时间是10 ![]() s;
s;
(3)火箭落回地面时的速度大小 v′=a′t′=3×10 ![]() =30
=30 ![]() m/s
m/s
答:火箭落回地面时的速度大小是30 ![]() m/s.
m/s.
【解析】(1)在v﹣t图象中,倾斜的直线表示匀变速直线运动,斜率表示加速度,图象与坐标轴围成的面积表示位移,由此求解.(2)火箭由最大高度处至落回地面的过程中通过的位移与上升的位移大小相等,由位移时间公式求解.(3)由速度时间公式求火箭落回地面时的速度大小.
【考点精析】利用V-t图象对题目进行判断即可得到答案,需要熟知v-t图像:①在速度图像中,可以读出物体在任何时刻的速度;②在速度图像中,物体在一段时间内的位移大小等于物体的速度图像与这段时间轴所围面积的值;③在速度图像中,物体在任意时刻的加速度就是速度图像上所对应的点的切线的斜率;④图线与横轴交叉,表示物体运动的速度反向;⑤图线是直线表示物体做匀变速直线运动或匀速直线运动;图线是曲线表示物体做变加速运动.

 中考解读考点精练系列答案
中考解读考点精练系列答案【题目】某同学在做“探究弹力与弹簧伸长量之间的关系”的实验时,所用实验装置如图1所示,所用的钩码每只的质量都是30g,他先测出不挂钩码时弹簧的自然长度,再将5个钩码逐个挂在弹簧的下端,每次都测出相应的弹簧总长度,将数据填在了下面的表中.(弹簧始终未超过弹性限度,取g=10m/s2)
钩码质量/g | 0 | 30 | 60 | 90 | 120 | 150 |
弹簧总长/cm | 6.00 | 7.00 | 8.00 | 9.00 | 10.00 | 11.00 |

(1)在图2坐标纸上作出弹簧所受弹力大小F跟弹簧总长x之间的函数关系图线.
(2)由图象求得图线斜率为;该图线的数学表达式F= .