题目内容
5.A、B两个质点分别做匀速圆周运动,经过相同的时间,它们通过的弧长之比SASB=4:3,半径经过的角度之比θ:θ=3:2,则它们的线速度之比VA:VB=4:3,周期之比TA:TB=2:3,向心加速度大小之比为aA:aB=2:1.分析 根据公式v=$\frac{s}{t}$ 求解线速度之比,根据公式ω=$\frac{θ}{t}$求解角速度之比,根据公式T=$\frac{2π}{ω}$求周期之比,根据an=ωv,即可求解加速度之比.
解答 解:A、B两质点分别做匀速圆周运动,若在相等时间内它们通过的弧长之比为SA:SB=4:3,
根据公式公式v=$\frac{s}{t}$,线速度之比为:vA:vB=4:3;
B、通过的圆心角之比θA:θB=3:2,根据公式ω=$\frac{θ}{t}$,角速度之比为3:2;
由根据公式T=$\frac{2π}{ω}$,周期之比为:TA:TB=2:3;
根据an=ωv,可知aA:aB=2:1;
故答案为:4:3,2:3,2:1.
点评 本题关键是记住线速度、角速度、周期和向心加速度的公式,根据公式列式分析,基础题.

练习册系列答案
相关题目
16.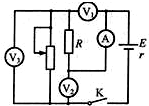 如图所示,将电路中的滑动变阻器滑片向上滑动,理想电压表V1、V2、V3示数变化量的大小分别为△U1、△U2、△U3,理想电流表A示数变化量的大小为△I,则( )
如图所示,将电路中的滑动变阻器滑片向上滑动,理想电压表V1、V2、V3示数变化量的大小分别为△U1、△U2、△U3,理想电流表A示数变化量的大小为△I,则( )
 如图所示,将电路中的滑动变阻器滑片向上滑动,理想电压表V1、V2、V3示数变化量的大小分别为△U1、△U2、△U3,理想电流表A示数变化量的大小为△I,则( )
如图所示,将电路中的滑动变阻器滑片向上滑动,理想电压表V1、V2、V3示数变化量的大小分别为△U1、△U2、△U3,理想电流表A示数变化量的大小为△I,则( )| A. | V2的示数减小 | B. | A的示数减小 | ||
| C. | △U1大于△U2 | D. | △U3与△I的比值大于r |
20.下面生活、生产中常见的事例,应用牛顿第三定律的是( )
①小船靠划桨而前进
②帆船利用风吹来航行
③喷气式飞机向后喷出燃气推动飞机前进
④潜艇水下航行是靠尾部螺旋桨工作向后推压水使之前进的.
①小船靠划桨而前进
②帆船利用风吹来航行
③喷气式飞机向后喷出燃气推动飞机前进
④潜艇水下航行是靠尾部螺旋桨工作向后推压水使之前进的.
| A. | 只有①③是应用牛顿第三定律 | B. | 只有②④是应用牛顿第三定律 | ||
| C. | ①②③是应用牛顿第三定律 | D. | ①③④是应用牛顿第三定律 |
10.物体朝某一方向做直线运动,前$\frac{1}{3}$位移内的平均速度是v1,后$\frac{2}{3}$位位移的平均速度是v2,则该物体在整个运动中的平均速度是( )
| A. | $\frac{{{v_1}{v_2}}}{{{v_1}+{v_2}}}$ | B. | $\frac{{2{v_1}{v_2}}}{{{v_1}+{v_2}}}$ | C. | $\frac{{3{v_1}{v_2}}}{{2{v_1}+{v_2}}}$ | D. | $\frac{{{v_1}+{v_2}}}{2}$ |
14. 如图所示,闭合开关S,待电容器充电结束后,再断开开关S,用绝缘工具使电容器两极板距离稍稍拉开一些,在电容器周围空间( )
如图所示,闭合开关S,待电容器充电结束后,再断开开关S,用绝缘工具使电容器两极板距离稍稍拉开一些,在电容器周围空间( )
 如图所示,闭合开关S,待电容器充电结束后,再断开开关S,用绝缘工具使电容器两极板距离稍稍拉开一些,在电容器周围空间( )
如图所示,闭合开关S,待电容器充电结束后,再断开开关S,用绝缘工具使电容器两极板距离稍稍拉开一些,在电容器周围空间( )| A. | 会产生变化的磁场 | B. | 会产生稳定的磁场 | ||
| C. | 不会产生磁场 | D. | 会产生振荡的磁场 |
15.下列叙述中,正确的是( )
| A. | 磁场对静止电荷和运动电荷都有力的作用 | |
| B. | 磁感线从磁体的N极出发到磁体的S极终止 | |
| C. | 磁感线上某点的切线方向与小磁针在该点N极的受力方向相同 | |
| D. | 以上说法均不正确 |
 一个研究摩擦力的简单模型,由一个劈与小球组成.如下图所示:一个底面粗糙,质量为M的斜面体静止在水平地面上,斜面体斜面是光滑的,倾角为30度,现用质量为M的斜面体静止在水平地面上,斜面体斜面是光滑的,倾角为30度,现用一端固定的轻绳系一质量为m的小球,小球静止时轻绳与斜面的夹角是30度.现在劈刚能保持静止状态,如果近似认为最大静摩擦力等于滑动摩擦力,求
一个研究摩擦力的简单模型,由一个劈与小球组成.如下图所示:一个底面粗糙,质量为M的斜面体静止在水平地面上,斜面体斜面是光滑的,倾角为30度,现用质量为M的斜面体静止在水平地面上,斜面体斜面是光滑的,倾角为30度,现用一端固定的轻绳系一质量为m的小球,小球静止时轻绳与斜面的夹角是30度.现在劈刚能保持静止状态,如果近似认为最大静摩擦力等于滑动摩擦力,求