题目内容
 如图所示,一个带负电的粒子以速度v由坐标原点射入磁感应强度为B的匀强磁场中,速度方向与x轴、y轴均成45°.已知该粒子电量为-q,质量为m,则该粒子通过x轴和y轴的坐标分别是多少?
如图所示,一个带负电的粒子以速度v由坐标原点射入磁感应强度为B的匀强磁场中,速度方向与x轴、y轴均成45°.已知该粒子电量为-q,质量为m,则该粒子通过x轴和y轴的坐标分别是多少?分析:首先根据左手定则判断洛伦兹力的方向,从而得知带电粒子的旋转方向,画出运动的轨迹图,利用圆周运动的半径公式结合几何关系可求出经过x轴和y轴的坐标.
解答:解: 因粒子带负电,由左手定则可判断出带电粒子将沿顺时针方向转动,轨迹如图所示,运动轨迹的半径为:
因粒子带负电,由左手定则可判断出带电粒子将沿顺时针方向转动,轨迹如图所示,运动轨迹的半径为:
R=
因射入时与x轴的方向成45°角,由几何关系可知,带电粒子通过x轴时,转过了90°角,此时的坐标为:
x=
=
同理可知,粒子经过y轴时,转过了270°角.此时的坐标为:
y=-
=-
答:粒子通过x轴和y轴的坐标分别是
,-
.
 因粒子带负电,由左手定则可判断出带电粒子将沿顺时针方向转动,轨迹如图所示,运动轨迹的半径为:
因粒子带负电,由左手定则可判断出带电粒子将沿顺时针方向转动,轨迹如图所示,运动轨迹的半径为:R=
| mv |
| qB |
因射入时与x轴的方向成45°角,由几何关系可知,带电粒子通过x轴时,转过了90°角,此时的坐标为:
x=
| R2+R2 |
| 2 |
| mv |
| qB |
同理可知,粒子经过y轴时,转过了270°角.此时的坐标为:
y=-
| R2+R2 |
| 2 |
| mv |
| qB |
答:粒子通过x轴和y轴的坐标分别是
| 2 |
| mv |
| qB |
| 2 |
| mv |
| qB |
点评:带电粒子做匀速圆周运动的圆心、半径及运动时间的确定:
圆心的确定:因洛伦兹力提供向心力,洛伦兹力总垂直于速度,画出带电粒子运动轨迹中任意两点(一般是射入磁场和射出磁场的两点)洛伦兹力的方向,其延长的交点即为圆心.或射入磁场和射出磁场的两点间弦的垂直平分线与一半径的交点即为圆心.
半径的确定:半径一般都在确定圆心的基础上用平面几何知识求解,常常是解直角三角形.
运动时间的确定:利用圆心与弦切角的关系计算出粒子所转过的圆心角θ的大小,用公式t=
T可求出运动时间.
圆心的确定:因洛伦兹力提供向心力,洛伦兹力总垂直于速度,画出带电粒子运动轨迹中任意两点(一般是射入磁场和射出磁场的两点)洛伦兹力的方向,其延长的交点即为圆心.或射入磁场和射出磁场的两点间弦的垂直平分线与一半径的交点即为圆心.
半径的确定:半径一般都在确定圆心的基础上用平面几何知识求解,常常是解直角三角形.
运动时间的确定:利用圆心与弦切角的关系计算出粒子所转过的圆心角θ的大小,用公式t=
| θ |
| 360 |

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
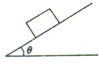 如图所示,一个带负电的物体由粗糙绝缘的斜面顶端自静止下滑到底端时速度为v,若加一个垂直于纸面向外的匀强磁场,则带电体滑到底端时速度将( )
如图所示,一个带负电的物体由粗糙绝缘的斜面顶端自静止下滑到底端时速度为v,若加一个垂直于纸面向外的匀强磁场,则带电体滑到底端时速度将( ) 如图所示,一个带负电的粒子沿着逆时针方向作匀速圆周运动,则此粒子的运动( )
如图所示,一个带负电的粒子沿着逆时针方向作匀速圆周运动,则此粒子的运动( ) 等量、同种、带正电的点电荷的连线和其中垂线如图所示.一个带负电的试探电荷,先从图中a点沿直线移到b点,再从b点沿直线移到c点,则( )
等量、同种、带正电的点电荷的连线和其中垂线如图所示.一个带负电的试探电荷,先从图中a点沿直线移到b点,再从b点沿直线移到c点,则( ) 等量、同种、带正电的点电荷的连线和其中垂线如图所示.一个带负电的试探电荷,先从图中a点沿直线移到b点,再从b点沿直线移到c点,则( )
等量、同种、带正电的点电荷的连线和其中垂线如图所示.一个带负电的试探电荷,先从图中a点沿直线移到b点,再从b点沿直线移到c点,则( )