题目内容
14.21世纪,我国某宇航员登上一半径为R的球状星体,宇航员在该星体上用常规方法就能测量出该星球的质量.在星球表面上,两次用相同的力竖直上抛和平抛同一物体,使两次抛出时的初速度速率相等,用停表测出从竖直上抛到落回抛出点的总时间t0,再用卷尺测出平抛的水平射程x和下落高度h.已知该星球的半径为R,且物体只受该星球的引力作用.(1)求该星球表面的重力加速度.
(2)该宇航员如何计算该星球的质量?
(3)如果要在这个星球上发射一颗贴近它表面运行的卫星,求该卫星做匀速圆周运动的线速度和周期.
分析 由平抛运动和竖直上抛运动规律求解重力加速度;
根据在星球表面星球与宇航员的万有引力近似等于宇航员的重力列出等式求解星球的质量;
根据万有引力提供向心力求解线速度和周期.
解答 解:(1)由平抛运动知识得x=v0t,
h=$\frac{1}{2}$gt2消去t得:g=$\frac{{v}_{0}^{2}}{{x}^{2}}$•2h…①
由竖直上抛运动知识得:v0=g•$\frac{{t}_{0}}{2}$,
②将②代入①消去v0得:g=$\frac{{2x}^{2}}{{ht}_{0}^{2}}$
(2)根据在星球表面星球与宇航员的万有引力近似等于宇航员的重力,有:
$\frac{GMm}{{R}^{2}}$=mg,
可知:M=$\frac{{gR}^{2}}{G}$.
该星球的质量为:M=$\frac{{{2x}^{2}R}^{2}}{G{ht}_{0}^{2}}$,
(3)该卫星做匀速圆周运动的线速度为:v=$\sqrt{\frac{GM}{R}}$=$\frac{x}{{t}_{0}}$$\sqrt{\frac{2R}{h}}$
周期为:T=$\frac{2πR}{v}$=$\frac{{πt}_{0}}{x}$$\sqrt{2hR}$,
答:(1)该星球表面的重力加速度是$\frac{{2x}^{2}}{{ht}_{0}^{2}}$.
(2)该星球的质量是$\frac{{{2x}^{2}R}^{2}}{G{ht}_{0}^{2}}$.
(3)该卫星做匀速圆周运动的线速度是$\frac{x}{{t}_{0}}$$\sqrt{\frac{2R}{h}}$,周期是$\frac{{πt}_{0}}{x}$$\sqrt{2hR}$.
点评 计算星球的质量主要从星球表面重力与万有引力等,或万有引力提供环绕天体圆周运动的向心力出发计算.

| A. | 子弹原有的动能全部转化为子弹和木块的内能 | |
| B. | 子弹损失的动能等于子弹克服阻力所做的功,即F(d+s) | |
| C. | 木块与子弹组成的系统产生的热能为Q=Fs | |
| D. | 子弹击中木块后,木块一直做匀加速运动 |
| A. | 两个直线运动的合运动一定也是直线运动 | |
| B. | 两个匀速直线运动的合运动一定也是匀速直线运动 | |
| C. | 两个匀变速直线运动的合运动一定也是匀变速直线运动 | |
| D. | 一个匀速直线运动和一个匀变速直线运动的合运动一定是曲线运动 |
 横截面为直角三角形的两个相同斜面紧靠在一起,固定在水平面上,如图所示.现有三个小球从左边斜面的顶点以不同的初速度向右平抛,最后落在斜面上.其落点分别是a、b、c.下列判断正确的是( )
横截面为直角三角形的两个相同斜面紧靠在一起,固定在水平面上,如图所示.现有三个小球从左边斜面的顶点以不同的初速度向右平抛,最后落在斜面上.其落点分别是a、b、c.下列判断正确的是( )| A. | 图中三小球比较,落在a点的小球飞行时间最短 | |
| B. | 图中三小球比较,落在c点的小球飞行时间最短 | |
| C. | 图中三小球比较,落在c点的小球飞行过程速度变化最大 | |
| D. | 图中三小球比较,落在c点的小球飞行过程速度变化最快 |
 如图所示是一个单摆做受迫振动时的共振曲线,表示振幅A与驱动力的频率f的关系,下列说法正确的是( )
如图所示是一个单摆做受迫振动时的共振曲线,表示振幅A与驱动力的频率f的关系,下列说法正确的是( )| A. | 若增大摆长,共振曲线的“峰”将向右移动 | |
| B. | 若改变摆长,共振曲线的“峰”将不会移动 | |
| C. | 该单摆的摆长约为1 m | |
| D. | 若将该单摆移到月球上,其共振曲线的“峰”将向右移动 |
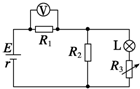 如图所示,R1、R2为定值电阻,L为小灯泡,R3为光敏电阻,当照射光强度增大时电压表的示数增大,下列说法不正确的是( )
如图所示,R1、R2为定值电阻,L为小灯泡,R3为光敏电阻,当照射光强度增大时电压表的示数增大,下列说法不正确的是( )| A. | 电压表的示数增大,表明光敏电阻具有随光照增强阻值要增大的特性 | |
| B. | R2中电流减小 | |
| C. | 小灯泡的功率增大 | |
| D. | 电路的路端电压增大 |
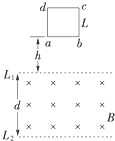 如图所示,相距为d的两水平虚线L1、L2之间有方向垂直纸面向里的匀强磁场,磁感应强度为B,正方形线圈abcd的边长为L(L<d)、质量为m、电阻为R.现将线圈在磁场上方高h处由静止释放,ab边刚进入磁场时的速度和刚离开磁场时的速度相同,在线圈全部穿过磁场过程中,下列说法正确的是( )
如图所示,相距为d的两水平虚线L1、L2之间有方向垂直纸面向里的匀强磁场,磁感应强度为B,正方形线圈abcd的边长为L(L<d)、质量为m、电阻为R.现将线圈在磁场上方高h处由静止释放,ab边刚进入磁场时的速度和刚离开磁场时的速度相同,在线圈全部穿过磁场过程中,下列说法正确的是( )| A. | 线圈克服安培力所做的功为2mgL | B. | 线圈克服安培力所做的功为2mgd | ||
| C. | 线圈的最小速度可能为$\frac{mgR}{{B}^{2}{L}^{2}}$ | D. | 线圈的最小速度一定为$\sqrt{2g(h+L-d)}$ |
| A. | 根据玻尔理论,氢原子在辐射光子的同时,轨道半径也在连续地减小 | |
| B. | 根据玻尔理论,氢原子的核外电子由较高能级跃迁到较低能级时,要释放一定频率的光子,同时电子的动能增大,电势能减小 | |
| C. | 同一元素的两种同位素具有相同的质子数 | |
| D. | 某放射性原子核经过3次α衰变和一次β衰变,核内质子数减少3个 |
 如图所示,在水平向右的匀强电场中,一长为L的细线,上端固定于O点,下端拴一质量为m、电荷量为+q的小球.已知小球在A点处于静止状态,且细线与水平方向的夹角为30°,求:
如图所示,在水平向右的匀强电场中,一长为L的细线,上端固定于O点,下端拴一质量为m、电荷量为+q的小球.已知小球在A点处于静止状态,且细线与水平方向的夹角为30°,求: