题目内容
5. 如图所示,在水平向右的匀强电场中,一长为L的细线,上端固定于O点,下端拴一质量为m、电荷量为+q的小球.已知小球在A点处于静止状态,且细线与水平方向的夹角为30°,求:
如图所示,在水平向右的匀强电场中,一长为L的细线,上端固定于O点,下端拴一质量为m、电荷量为+q的小球.已知小球在A点处于静止状态,且细线与水平方向的夹角为30°,求:(1)匀强电场的场强E的大小;
(2)若将小球拉至水平位置B,由静止释放,求小球经过A点时的速度v的大小;
(3)小球经过A点后速度再次为零时,细线与水平方向的夹角θ.
分析 (1)小球在电场中受到重力、水平向右的电场力和细线的拉力而平衡,作出力图,由平衡条件求解场强的大小.
(2)从B运动到A,由动能定理求小球经过A点时的速度v的大小.
(3)小球经过A点后速度再次为零时,运用动能定理求细线与水平方向的夹角θ.
解答 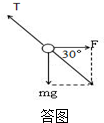 解:(1)分析小球的受力情况:小球在电场中受到重力、水平向右的电场力F和细线的拉力T.作出力图,如图.
解:(1)分析小球的受力情况:小球在电场中受到重力、水平向右的电场力F和细线的拉力T.作出力图,如图.
根据平衡条件得
Ftan30°=mg
又 F=qE
解得 E=$\frac{\sqrt{3}mg}{q}$
(2)从B运动到A,由动能定理得
mgLsin30°-qEL(1-cos30°)=$\frac{1}{2}m{v}_{A}^{2}$
解得 vA=$\sqrt{(4-2\sqrt{3})gL}$
(3)根据动能定理得:mgLsinθ-qEL(1-cosθ)=0
代入得:Lsinθ-$\sqrt{3}$L(1-$\sqrt{1-si{n}^{2}θ}$)=0
解得θ=arcsin$\frac{\sqrt{3}}{4}$
答:
(1)匀强电场的场强E的大小为$\frac{\sqrt{3}mg}{q}$;
(2)若将小球拉至水平位置B,由静止释放,小球经过A点时的速度v的大小为$\sqrt{(4-2\sqrt{3})gL}$;
(3)小球经过A点后速度再次为零时,细线与水平方向的夹角θ为arcsin$\frac{\sqrt{3}}{4}$.
点评 本题是电场中物体的平衡问题和复合场中的竖直平面内圆周运动问题,按照力学的方法和思路,把电场力当作一般的力处理,问题就变得容易,要明确涉及力在空间的效果首先要想到动能定理.

练习册系列答案
相关题目
15. 如图所示,小球自a点由静止自由下落,到b点时与弹簧接触,到c点时弹簧被压缩到最短,若不计弹簧质量和空气阻力,在小球由a→b→c的运动过程中( )
如图所示,小球自a点由静止自由下落,到b点时与弹簧接触,到c点时弹簧被压缩到最短,若不计弹簧质量和空气阻力,在小球由a→b→c的运动过程中( )
 如图所示,小球自a点由静止自由下落,到b点时与弹簧接触,到c点时弹簧被压缩到最短,若不计弹簧质量和空气阻力,在小球由a→b→c的运动过程中( )
如图所示,小球自a点由静止自由下落,到b点时与弹簧接触,到c点时弹簧被压缩到最短,若不计弹簧质量和空气阻力,在小球由a→b→c的运动过程中( )| A. | 小球的加速度在ab段不变,在bc段逐渐减小 | |
| B. | 小球的重力势能减少 | |
| C. | 小球在b点时速度最大 | |
| D. | 小球的机械能守恒 |
16.行星A绕太阳的运动视为匀速做圆周运动,其运行轨道半径为r,周期为T.观察发现,其实际运行的轨道与圆轨道存在一些偏离,且每隔时间t发生一次最大的偏离(计算时仍看成圆周运动).形成这种现象的原因可能是行星A外侧还存在着一颗未知行星B,它对行星A的万有引力引起A行星轨道的偏离,且行星A的轨道发生最大偏离时,A、B两行星相距最近.根据这些条件,可求得行星B的轨道半径为( )
| A. | ($\frac{t-T}{t}$)${\;}^{\frac{2}{3}}$r | B. | $\frac{t}{t-T}$r | C. | ($\frac{t}{t-T}$)${\;}^{\frac{2}{3}}$r | D. | ($\frac{t}{t+T}$)${\;}^{\frac{2}{3}}$r |
13.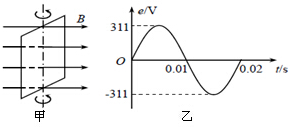 在匀强磁场中,一矩形金属线框绕与磁感线垂直的转轴匀速转动,如图甲所示,产生的交变电动势的图象如图乙所示,则( )
在匀强磁场中,一矩形金属线框绕与磁感线垂直的转轴匀速转动,如图甲所示,产生的交变电动势的图象如图乙所示,则( )
 在匀强磁场中,一矩形金属线框绕与磁感线垂直的转轴匀速转动,如图甲所示,产生的交变电动势的图象如图乙所示,则( )
在匀强磁场中,一矩形金属线框绕与磁感线垂直的转轴匀速转动,如图甲所示,产生的交变电动势的图象如图乙所示,则( )| A. | t=0.015s时穿过线框的磁通量变化率为零 | |
| B. | t=0.01s时线框平面与中性面重合 | |
| C. | 线框产生的交变电动势有效值为311V | |
| D. | 线框产生的交变电动势频率为100Hz |
20.甲乙两个做匀速圆周运动的质点,它们的角速度之比为3:1,线速度之比为2:3,质量之比为1:1,那么下列说法中正确的是( )
| A. | 它们的半径之比是2:3 | B. | 它们的向心加速度之比为2:1 | ||
| C. | 它们的周期之比为3:1 | D. | 它们的向心力之比为1:2 |
17.如图所示的a、b、c、d中,质量为M的物体甲受到相同的恒力F的作用,在力F作用下使物体甲在水平方向移动相同的位移.μ表示物体甲与水平面间的动摩擦因数,乙是随物体甲一起运动的小物块,比较物体甲移动的过程中力F对甲所做的功的大小( )


| A. | Wa最小 | B. | Wd最大 | C. | Wa=Wc | D. | 四种情况一样大 |
15.如图所示是行星m绕恒星M运动情况的示意图,则下列说法正确的是( )


| A. | 速度最大是在B点 | B. | 速度最大是在A点 | ||
| C. | m从A到B做减速运动 | D. | m从B到A做减速运动 |
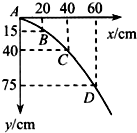 在做研究平抛运动的实验时,让小球多次沿同一轨道运动,通过描点法画出小球平抛运动的轨迹.
在做研究平抛运动的实验时,让小球多次沿同一轨道运动,通过描点法画出小球平抛运动的轨迹.