题目内容
16.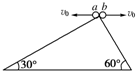 如图所示,两小球a、b从直角三角形斜面的顶端以相同大小的水平速率v0向左、向右水平抛出,分别落在两个斜面上,三角形的两底角分别为30°和60°,则两小球a、b落到斜面时的速度之比为( )
如图所示,两小球a、b从直角三角形斜面的顶端以相同大小的水平速率v0向左、向右水平抛出,分别落在两个斜面上,三角形的两底角分别为30°和60°,则两小球a、b落到斜面时的速度之比为( )| A. | $\sqrt{7}$:$\sqrt{39}$ | B. | $\sqrt{39}$:$\sqrt{7}$ | C. | 1:$\sqrt{3}$ | D. | 1:3 |
分析 熟练应用平抛运动过程中位移与水平方向夹角θ的表达式:tanθ=$\frac{y}{x}$,求出时间,得到竖直方向的分速度,然后根据速度的合成求出物体落地速度,再求出速度之比.
解答 解:小球落到斜面上时有:tanθ=$\frac{y}{x}$=$\frac{\frac{1}{2}g{t}^{2}}{{v}_{0}t}$=$\frac{gt}{2{v}_{0}}$=$\frac{{v}_{y}}{2{v}_{0}}$,
竖直方向速度为 vy=gt=2v0tanθ,
物体落到斜面上的速度:v=$\sqrt{{v}_{0}^{2}+{v}_{y}^{2}}$=v0$\sqrt{1+4ta{n}^{2}θ}$,
小球a、b落到斜面时的速度之比:$\frac{{v}_{a}}{{v}_{b}}$=$\frac{{v}_{0}\sqrt{1+4(tan30°)^{2}}}{{v}_{0}\sqrt{1+4(tan60°)^{2}}}$=$\frac{\sqrt{7}}{\sqrt{39}}$;
故选:A.
点评 平抛运动中速度与水平方向,位移与水平方向之间夹角的表达式以及它们之间的关系是经常考查的重点,要加强练习和应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.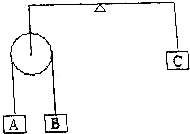 如图所示,等臂天平左端挂一质量不计的光滑定滑轮,跨过滑轮的轻绳,两端各拴一物体A和B,已知物体B的质量mB=3kg,欲使天平平衡,物体C的质量可能是( )
如图所示,等臂天平左端挂一质量不计的光滑定滑轮,跨过滑轮的轻绳,两端各拴一物体A和B,已知物体B的质量mB=3kg,欲使天平平衡,物体C的质量可能是( )
 如图所示,等臂天平左端挂一质量不计的光滑定滑轮,跨过滑轮的轻绳,两端各拴一物体A和B,已知物体B的质量mB=3kg,欲使天平平衡,物体C的质量可能是( )
如图所示,等臂天平左端挂一质量不计的光滑定滑轮,跨过滑轮的轻绳,两端各拴一物体A和B,已知物体B的质量mB=3kg,欲使天平平衡,物体C的质量可能是( )| A. | 3kg | B. | 9kg | C. | 12kg | D. | 15kg |
7.从同一地点出发,甲、乙两个物体沿同一方向做直线运动的速度-时间图象如图所示,则( )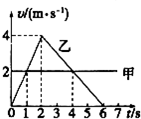

| A. | 两物体相遇的时间是2s和6s | |
| B. | 乙物体先向前运动2s,随后向后运动 | |
| C. | 前6s内两个物体的最大距离是2m | |
| D. | 4s后甲在乙前面 |
1.人造地球卫星绕地球做匀速圆周运动,当运行轨道半径变小时,下列说法错误的是( )
| A. | 它的线速度变大 | B. | 它的角速度变小 | ||
| C. | 它的加速度变大 | D. | 它的运行周期变小 |
8. 如图所示为汽车在水平路面上启动过程的v-t图象.0~t1时间内为匀加速阶段,t1~t2时间内表示以额定功率行驶时的变加速阶段,t2后是与t轴平行的直线,则下列说法正确的是( )
如图所示为汽车在水平路面上启动过程的v-t图象.0~t1时间内为匀加速阶段,t1~t2时间内表示以额定功率行驶时的变加速阶段,t2后是与t轴平行的直线,则下列说法正确的是( )
 如图所示为汽车在水平路面上启动过程的v-t图象.0~t1时间内为匀加速阶段,t1~t2时间内表示以额定功率行驶时的变加速阶段,t2后是与t轴平行的直线,则下列说法正确的是( )
如图所示为汽车在水平路面上启动过程的v-t图象.0~t1时间内为匀加速阶段,t1~t2时间内表示以额定功率行驶时的变加速阶段,t2后是与t轴平行的直线,则下列说法正确的是( )| A. | 0~t1时间内,牵引力不变,功率增大 | |
| B. | 0~t1时间内,牵引力增大,功率不变 | |
| C. | t1~t2时间内,牵引力增大,加速度减小 | |
| D. | t1~t2时间内,牵引力做的功为$\frac{1}{2}$mv22-$\frac{1}{2}$mv12 |
5. 如图所示,某同学在做“探究弹簧伸长量与弹力的关系”实验时,先测出不挂钩码时弹簧的长度L0=20.00cm,然后在弹簧的下端依次挂上不同个数规格相同的钩码,测出每次相应的弹簧长度L,得到下面的记录表格.
如图所示,某同学在做“探究弹簧伸长量与弹力的关系”实验时,先测出不挂钩码时弹簧的长度L0=20.00cm,然后在弹簧的下端依次挂上不同个数规格相同的钩码,测出每次相应的弹簧长度L,得到下面的记录表格.
(1)当弹力大小为0.98N时,弹簧伸长量为4.00cm;
(2)由实验可知,在弹性限度内,弹簧的弹力与弹簧的伸长量成正比(选填“正比”或“反比”);
(3)由表中数据,可求出该弹簧的劲度系数为24.5N/m.
 如图所示,某同学在做“探究弹簧伸长量与弹力的关系”实验时,先测出不挂钩码时弹簧的长度L0=20.00cm,然后在弹簧的下端依次挂上不同个数规格相同的钩码,测出每次相应的弹簧长度L,得到下面的记录表格.
如图所示,某同学在做“探究弹簧伸长量与弹力的关系”实验时,先测出不挂钩码时弹簧的长度L0=20.00cm,然后在弹簧的下端依次挂上不同个数规格相同的钩码,测出每次相应的弹簧长度L,得到下面的记录表格.| 次数 | 弹簧的长度 L/cm | 弹簧伸长量 x/cm | 弹力大小 F/N |
| 1 | 22.00 | 2.00 | 0.49 |
| 2 | 24.00 | 0.98 | |
| 3 | 26.00 | 6.00 | l.47 |
| 4 | 28.01 | 8.01 | 1.96 |
| 5 | 29.98 | 9.98 | 2.45 |
(2)由实验可知,在弹性限度内,弹簧的弹力与弹簧的伸长量成正比(选填“正比”或“反比”);
(3)由表中数据,可求出该弹簧的劲度系数为24.5N/m.

 如图所示,一质量为1kg的物体,位于距地面高h=20m倾角为θ的光滑斜面上,从静止开始下滑.已知物体与水平地面间的动摩擦因数μ=0.2,且经B点时无能量损失,最后滑到C点停止.(g取10m/s2) 求:
如图所示,一质量为1kg的物体,位于距地面高h=20m倾角为θ的光滑斜面上,从静止开始下滑.已知物体与水平地面间的动摩擦因数μ=0.2,且经B点时无能量损失,最后滑到C点停止.(g取10m/s2) 求: