题目内容
如图所示，匀强磁场中有一个带电量为q的离子自a点沿箭头方向运动．当它运动到b点时，突然吸收了附近的若干个电子，接着沿另一圆轨道运动到与a、b在一条直线上的c点．已知ac=| 1 |
| 2 |
分析：根据ac与ab的长度关系，可得知离子在吸收电子之前和吸收之后运动半径的变化，再由洛伦兹力提供向心力解出粒子做圆周运动的半径公式，根据公式判断出电量的变化情况．
解答：解：根据左手定则判断出粒子带正电，设ab等于2R，即粒子开始的轨道半径为R，后来的轨道半径为1.5R．
由洛伦兹力提供向心力得：qvB=
解得：R=
…①
第二个过程中：1.5R=
…②
由①②解得：q2=
q
所以电荷量减少了：△q=q-q2=
q…③
设吸收的电子个数为n，则有：△q=ne…④
③④联立得：n=
故选：D
由洛伦兹力提供向心力得：qvB=
| mv2 |
| R |
解得：R=
| mv |
| qB |
第二个过程中：1.5R=
| mv |
| q2B |
由①②解得：q2=
| 2 |
| 3 |
所以电荷量减少了：△q=q-q2=
| 1 |
| 3 |
设吸收的电子个数为n，则有：△q=ne…④
③④联立得：n=
| q |
| 3e |
故选：D
点评：带电离子在磁场中的运动问题，要注意可以根据洛伦兹力提供向心力解出粒子做圆周运动的轨道半径表达式，由于电量的改变而导致运动半径的变化，同时运动的周期也发生变化．
练习册系列答案
相关题目
用细线悬挂一个质量为m，带正电的小球，置于如图所示的匀强磁场中．当小球偏离竖直方向在垂直于磁场方向摆动时，如果细线始终绷紧，不计空气阻力，则前后两次通过最低点时相比较，相同的物理量是（ ）
如图所示，匀强磁场中有一个开口向上的绝缘半球，内壁粗糙程度处处相同，将带有正电荷的小球从半球左边最高处静止释放，物块沿半球内壁只能滑到右侧的C点处；如果撤去磁场，仍将小球从左边最高点释放，则滑到右侧最高点应是（ ）
在如图所示的匀强磁场中有一光滑的金属轨道，轨道上放有两根平行金属棒AB、CD．当棒AB向右平行移动时，棒CD将（ ）| A、保持静止 | B、向左运动 | C、向右运动 | D、发生转动 |
如图所示，匀强磁场中有一矩形闭合线圈abcd，线圈平面与磁场垂直．已知线圈的匝数N=100，边长ab=1.0m、bc=0.5m，电阻r=2Ω． 磁感应强度B在0～1s内从零均匀变化到0.2T． 在1～5s内从0.2T均匀变化到-0.2T，取垂直纸面向里为磁场的正方向．求：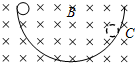
如图所示，匀强磁场中有一个开口向上的绝缘半球，内壁粗糙程度处处相同，将带有正电荷的小球（可视为质点）从半球左边最高处由静止释放，物块沿半球内壁只能滑到右侧的C点；如果撤去磁场，仍将小球从左边最高点由静止释放，则滑到右侧最高点应是（ ）