题目内容
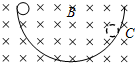如图所示，匀强磁场中有一个开口向上的绝缘半球，内壁粗糙程度处处相同，将带有正电荷的小球（可视为质点）从半球左边最高处由静止释放，物块沿半球内壁只能滑到右侧的C点；如果撤去磁场，仍将小球从左边最高点由静止释放，则滑到右侧最高点应是（ ）分析：有磁场时，带电小球要受到始终指向圆心的洛伦兹力作用，所以有磁场时，小球受到的轨道的支持力比没有磁场时要小，故有磁场时受到的摩擦力就小，再根据动能定理即可求解．
解答：解：有磁场：从左释放时，物块受到的洛伦兹力始终指向半球球心，物快对半球压力为N1，
撤去磁场：从右释放时，没有洛伦兹力，物快对半球压力为N2，
易知N1＜N2，故f1＜f2，所以若路程相等，则没有磁场时摩擦力f做的功比较大，
根据动能定理可知：
mg△h-Wf=0
所以高度比C点低．
故选C
撤去磁场：从右释放时，没有洛伦兹力，物快对半球压力为N2，
易知N1＜N2，故f1＜f2，所以若路程相等，则没有磁场时摩擦力f做的功比较大，
根据动能定理可知：
mg△h-Wf=0
所以高度比C点低．
故选C
点评：本题只要考查了带电小球在磁场中的受力问题，会根据左手定则判断洛伦兹力的方向且知道洛伦兹力用不做功．
练习册系列答案
中考解读考点精练系列答案
相关题目
用细线悬挂一个质量为m，带正电的小球，置于如图所示的匀强磁场中．当小球偏离竖直方向在垂直于磁场方向摆动时，如果细线始终绷紧，不计空气阻力，则前后两次通过最低点时相比较，相同的物理量是（ ）
如图所示，匀强磁场中有一个开口向上的绝缘半球，内壁粗糙程度处处相同，将带有正电荷的小球从半球左边最高处静止释放，物块沿半球内壁只能滑到右侧的C点处；如果撤去磁场，仍将小球从左边最高点释放，则滑到右侧最高点应是（ ）
在如图所示的匀强磁场中有一光滑的金属轨道，轨道上放有两根平行金属棒AB、CD．当棒AB向右平行移动时，棒CD将（ ）| A、保持静止 | B、向左运动 | C、向右运动 | D、发生转动 |
如图所示，匀强磁场中有一矩形闭合线圈abcd，线圈平面与磁场垂直．已知线圈的匝数N=100，边长ab=1.0m、bc=0.5m，电阻r=2Ω． 磁感应强度B在0～1s内从零均匀变化到0.2T． 在1～5s内从0.2T均匀变化到-0.2T，取垂直纸面向里为磁场的正方向．求：