题目内容
18.一艘宇宙飞船飞近某一新发现的行星,在离该行星中心距离为R的圆形轨道上做匀速圆周运动.现观测到此飞船环绕行星n圈所用的时间为t,已知引力常量为G,则此飞船绕该行星运动的周期为$\frac{t}{n}$,该行星的质量为$\frac{4{π}^{2}{n}^{2}{R}^{3}}{G{t}^{2}}$.分析 根据运动的时间和绕行的圈数求出飞船的周期,根据万有引力提供向心力求出行星的质量.
解答 解:飞船绕该行星运动的周期为:T=$\frac{t}{n}$,
根据$G\frac{Mm}{{R}^{2}}=mR\frac{4{π}^{2}}{{T}^{2}}$得行星的质量为:
M=$\frac{4{π}^{2}{R}^{3}}{G{T}^{2}}$=$\frac{4{π}^{2}{n}^{2}{R}^{3}}{G{t}^{2}}$.
故答案为:$\frac{t}{n}$,$\frac{4{π}^{2}{n}^{2}{R}^{3}}{G{t}^{2}}$.
点评 解决本题的关键掌握万有引力提供向心力这一重要理论,结合轨道半径和周期进行求解,基础题.

练习册系列答案
相关题目
18.如图所示为甲、乙两物体运动的x-t图象,则下列关于甲、乙两物体运动的说法,正确的是( )


| A. | 甲、乙两个物体同时出发 | B. | 甲、乙两个物体都做匀速直线运动 | ||
| C. | 甲的速度比乙的速度小 | D. | t2时刻两个物体速度相同 |
9.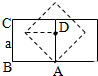 有一质量为m,边长为a的正方体与地面之间的摩擦因素μ=0.3.为使它水平移动距离a,可以采用将它翻倒或向前匀速平推两种方法.则( )
有一质量为m,边长为a的正方体与地面之间的摩擦因素μ=0.3.为使它水平移动距离a,可以采用将它翻倒或向前匀速平推两种方法.则( )
 有一质量为m,边长为a的正方体与地面之间的摩擦因素μ=0.3.为使它水平移动距离a,可以采用将它翻倒或向前匀速平推两种方法.则( )
有一质量为m,边长为a的正方体与地面之间的摩擦因素μ=0.3.为使它水平移动距离a,可以采用将它翻倒或向前匀速平推两种方法.则( )| A. | 将它翻倒比平推前进做的功少 | B. | 将它翻倒比平推前进做的功多 | ||
| C. | 两种情况做功一样多 | D. | 翻倒时不做功 |
3.如图,直线a和曲线b分别在平直公路上行驶的汽车a和b的位置-时间(x-t)图线.由图可知( )


| A. | 在t1时刻,a、b两车的运动方向相同 | |
| B. | 在t1到t2这段时间内,b车的平均速度比a车的大 | |
| C. | 在t1到t2这段时间内,b车的速率先减小后增大 | |
| D. | 在t1到t2这段时间内,b车的速率一直比a车大 |
7. 如图所示,为一比较两个电源输出功率的实验电路图,两个电源的电动势分别为E1和E2,内阻分别为r1和r2.单刀双掷开关置1或2时,调节电阻箱的阻值相同,两电源可能有相同的输出功率的是( )
如图所示,为一比较两个电源输出功率的实验电路图,两个电源的电动势分别为E1和E2,内阻分别为r1和r2.单刀双掷开关置1或2时,调节电阻箱的阻值相同,两电源可能有相同的输出功率的是( )
 如图所示,为一比较两个电源输出功率的实验电路图,两个电源的电动势分别为E1和E2,内阻分别为r1和r2.单刀双掷开关置1或2时,调节电阻箱的阻值相同,两电源可能有相同的输出功率的是( )
如图所示,为一比较两个电源输出功率的实验电路图,两个电源的电动势分别为E1和E2,内阻分别为r1和r2.单刀双掷开关置1或2时,调节电阻箱的阻值相同,两电源可能有相同的输出功率的是( )| A. | E1>E2、r1>r2 | B. | E1=E2、r1>r2 | C. | E1>E2、r1=r2 | D. | E1>E2、r1<r2 |
8. 一不计重力的带电粒子在匀强电场中的运动轨迹如图中虚线所示,等势面为一系列平行水平平面.若不计空气阻力,则此粒子从a运动到b的过程中,能量变化情况为( )
一不计重力的带电粒子在匀强电场中的运动轨迹如图中虚线所示,等势面为一系列平行水平平面.若不计空气阻力,则此粒子从a运动到b的过程中,能量变化情况为( )
 一不计重力的带电粒子在匀强电场中的运动轨迹如图中虚线所示,等势面为一系列平行水平平面.若不计空气阻力,则此粒子从a运动到b的过程中,能量变化情况为( )
一不计重力的带电粒子在匀强电场中的运动轨迹如图中虚线所示,等势面为一系列平行水平平面.若不计空气阻力,则此粒子从a运动到b的过程中,能量变化情况为( )| A. | 动能一定增加 | B. | 电势能一定增加 | ||
| C. | 动能和电势能之和一定增加 | D. | 动能和电势能之和一定不变 |
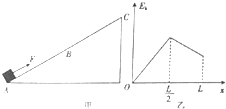 如图甲所示,将一块长度为$\frac{L}{2}$的表面光滑的金属板AB的另一块长度也为$\frac{L}{2}$的表面粗糙的木板BC平滑地拼接在一起组成斜面AC,并将一小物块在平行于斜面的恒定拉力F作用下由静止从A运动到C,历时为t0,小物块的动能Ek随位移x的变化情况如图乙所示,则小物块的速度v、加速度大小a、重力势能Ep随时间t(或位移x)变化情况的下列图中,可能正确的有( )
如图甲所示,将一块长度为$\frac{L}{2}$的表面光滑的金属板AB的另一块长度也为$\frac{L}{2}$的表面粗糙的木板BC平滑地拼接在一起组成斜面AC,并将一小物块在平行于斜面的恒定拉力F作用下由静止从A运动到C,历时为t0,小物块的动能Ek随位移x的变化情况如图乙所示,则小物块的速度v、加速度大小a、重力势能Ep随时间t(或位移x)变化情况的下列图中,可能正确的有( )