题目内容
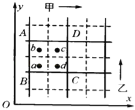
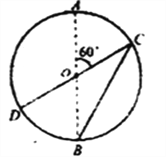
【题目】如图所示,AB为竖直平面内某圆周的竖直直径,CD为过O点且与AB成60°夹角的固定光滑细直杆,CB也为一固定光滑细直杆,两细直杆上各套有一个小球,小球可视为质点,两小球分别从C点由静止释放,小球从C点运动到D点所用的时间为t1,另一小球从C点运动到B点所用的时间为t2,则![]() 等于
等于
A. 1:1 B. 2:1 C. ![]() D.
D. ![]()
【答案】C
【解析】设AB=BC=d。小球从C点运动到D点的过程,由牛顿第二定律有 mgsin30°=ma1.得 a1=![]() g;由位移公式有 d=
g;由位移公式有 d=![]() a1t12;得 t1=
a1t12;得 t1=![]() ;小球从C点运动到B点的过程,由牛顿第二定律有 mgsin60°=ma1.得 a2=
;小球从C点运动到B点的过程,由牛顿第二定律有 mgsin60°=ma1.得 a2=![]() g;由位移公式有 dcos30°=
g;由位移公式有 dcos30°=![]() a1t12得 t2=
a1t12得 t2=![]() ,所以t1:t2=
,所以t1:t2=![]() :1,故选C。
:1,故选C。

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
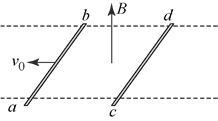
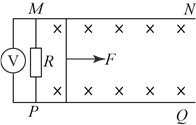
【题目】如图所示,光滑且足够长的平行金属导轨![]() 、
、![]() 固定在同一水平面上,两导轨间距
固定在同一水平面上,两导轨间距![]() ,电阻
,电阻![]() ,导轨上停放一质量
,导轨上停放一质量![]() 、电阻
、电阻![]() 的金属杆,导轨电阻可忽略不计,整个装置处于磁感应强度
的金属杆,导轨电阻可忽略不计,整个装置处于磁感应强度![]() 的匀强磁场中,磁场方向竖直向下,现用一外力
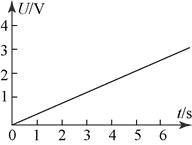
的匀强磁场中,磁场方向竖直向下,现用一外力![]() 沿水平方向拉杆,使之由静止开始运动,若理想电压表的示数
沿水平方向拉杆,使之由静止开始运动,若理想电压表的示数![]() 随时间
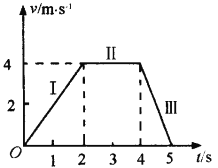
随时间![]() 变化的关系如图(
变化的关系如图(![]() )所示.
)所示.
|
|
图( | 图( |
(![]() )试分析说明金属杆的运动情况.
)试分析说明金属杆的运动情况.
(![]() )求第
)求第![]() 末外力
末外力![]() 的瞬时功率.
的瞬时功率.
(![]() )若在第
)若在第![]() 秒末撤去外力,从此时开始金属杆还能走多远.
秒末撤去外力,从此时开始金属杆还能走多远.