Question

如图所示，光滑水平面AB与竖直面内的半圆形轨道在B点相接，导轨半径为R.一个质量为m的物体将弹簧压缩至A点后由静止释放，在弹力作用下物体获得某一向右速度后脱离弹簧，脱离弹簧后当它经过B点进入导轨瞬间对导轨的压力为其重力的8倍，之后向上运动完成半个圆周运动恰好到达C点。试求：

（1）弹簧开始时的弹性势能；
（2）物体从B点运动至C点克服阻力做的功；
（3）物体离开C点后落回水平面时，重力的瞬时功率是多大？

Answer 1

（1）E_p=3.5mgR；（2）W_f，，=mgR；（3）

解析试题分析: (1)设弹簧的弹性势能为E_p，物体经过B点时的速度为，轨道对物体的支持力为N，，物体对轨道的压力为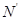由题意知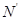=8mg      由机械能守恒得      E_p=m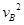
由牛顿第二定律得:  N-mg= 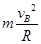      由牛顿第三定律得   N=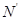
解得E_p=3.5mgR
(2)设物体克服阻力做功为W_f，，在C点速度为 ，
物体恰到达C点  mg= 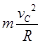    由动能定理得:  -2mgR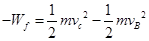
解得W_f，，=mgR
（3）物体落到水平面上时的竖直分速度是
重力的上升功率是P=mg
考点： 动能定理；机械能守恒定律