题目内容
如图甲所示,将质量为m的两个小球(可看成质点),用长为L的两根细软线拴连,线的上端连于O点且绕O点自由转动时与竖直方向夹角为θ。
 如图乙所示,将其中一质量为m的小球仍与一长为L的细绳连接,放在表面光滑的正圆锥体表面,上端可绕圆锥顶点自由转动。圆锥体放在水平面上,其轴线沿竖直方向,圆锥母线与轴线之间夹角α为30°,试求:
如图乙所示,将其中一质量为m的小球仍与一长为L的细绳连接,放在表面光滑的正圆锥体表面,上端可绕圆锥顶点自由转动。圆锥体放在水平面上,其轴线沿竖直方向,圆锥母线与轴线之间夹角α为30°,试求:
 (1)图甲中小球圆周运动的周期T=?
(1)图甲中小球圆周运动的周期T=?
 (2)图乙中当正圆锥体沿水平x轴方向匀加速运动的加速度a多大时,小球刚要离开锥面?
(2)图乙中当正圆锥体沿水平x轴方向匀加速运动的加速度a多大时,小球刚要离开锥面?
 (3)将图乙中与小球相连的细线穿过圆锥顶端的光滑小圆环后,与放在倾角β=37°的对称斜槽(斜槽两平面材料相同,与竖直面都成30°)里的质量为M的圆柱体相连,连接圆柱的细线平行斜槽的棱,如图丙所示。当小球以速度v=
(3)将图乙中与小球相连的细线穿过圆锥顶端的光滑小圆环后,与放在倾角β=37°的对称斜槽(斜槽两平面材料相同,与竖直面都成30°)里的质量为M的圆柱体相连,连接圆柱的细线平行斜槽的棱,如图丙所示。当小球以速度v=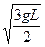 绕圆锥轴线做水平匀速圆周运动而圆柱M不动时,圆柱与两接触面间的摩擦因数μ至少多大?
绕圆锥轴线做水平匀速圆周运动而圆柱M不动时,圆柱与两接触面间的摩擦因数μ至少多大?


 如图乙所示,将其中一质量为m的小球仍与一长为L的细绳连接,放在表面光滑的正圆锥体表面,上端可绕圆锥顶点自由转动。圆锥体放在水平面上,其轴线沿竖直方向,圆锥母线与轴线之间夹角α为30°,试求:
如图乙所示,将其中一质量为m的小球仍与一长为L的细绳连接,放在表面光滑的正圆锥体表面,上端可绕圆锥顶点自由转动。圆锥体放在水平面上,其轴线沿竖直方向,圆锥母线与轴线之间夹角α为30°,试求: (1)图甲中小球圆周运动的周期T=?
(1)图甲中小球圆周运动的周期T=? (2)图乙中当正圆锥体沿水平x轴方向匀加速运动的加速度a多大时,小球刚要离开锥面?
(2)图乙中当正圆锥体沿水平x轴方向匀加速运动的加速度a多大时,小球刚要离开锥面? (3)将图乙中与小球相连的细线穿过圆锥顶端的光滑小圆环后,与放在倾角β=37°的对称斜槽(斜槽两平面材料相同,与竖直面都成30°)里的质量为M的圆柱体相连,连接圆柱的细线平行斜槽的棱,如图丙所示。当小球以速度v=
(3)将图乙中与小球相连的细线穿过圆锥顶端的光滑小圆环后,与放在倾角β=37°的对称斜槽(斜槽两平面材料相同,与竖直面都成30°)里的质量为M的圆柱体相连,连接圆柱的细线平行斜槽的棱,如图丙所示。当小球以速度v=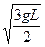 绕圆锥轴线做水平匀速圆周运动而圆柱M不动时,圆柱与两接触面间的摩擦因数μ至少多大?
绕圆锥轴线做水平匀速圆周运动而圆柱M不动时,圆柱与两接触面间的摩擦因数μ至少多大?

(1)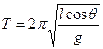 (2)
(2)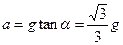 (3)
(3)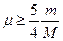
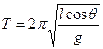 (2)
(2)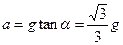 (3)
(3)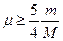
(1)对甲图中小球由向心力公式: 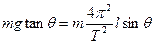
 得:
得: 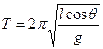
 (2)对乙图中小球,由牛顿定律得:
(2)对乙图中小球,由牛顿定律得: 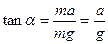
 所以:
所以: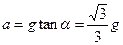
 (3)设小球刚好飞起的临界速度为v0,由(2)可得:
(3)设小球刚好飞起的临界速度为v0,由(2)可得:





















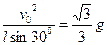 ,则
,则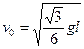
 因
因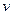 >
>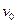 ,所以小球已经飞离锥面。设细线与水平方向成γ角。
,所以小球已经飞离锥面。设细线与水平方向成γ角。

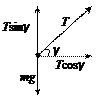 则有:
则有: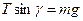

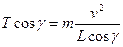
 可得:
可得: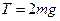

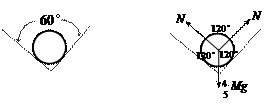
 垂直圆柱端面看:圆柱受力如图所示:两支持力N对称大小相等,且与重力Mg的垂直棱的分力Mgcos37°互成120°,则有:
垂直圆柱端面看:圆柱受力如图所示:两支持力N对称大小相等,且与重力Mg的垂直棱的分力Mgcos37°互成120°,则有:

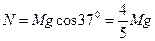
 由不滑动的条件有:
由不滑动的条件有: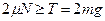
 所以:
所以: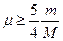

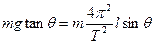

 得:
得: 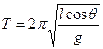
 (2)对乙图中小球,由牛顿定律得:
(2)对乙图中小球,由牛顿定律得: 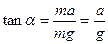
 所以:
所以: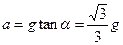
 (3)设小球刚好飞起的临界速度为v0,由(2)可得:
(3)设小球刚好飞起的临界速度为v0,由(2)可得:





















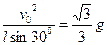 ,则
,则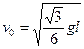
 因
因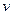 >
>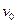 ,所以小球已经飞离锥面。设细线与水平方向成γ角。
,所以小球已经飞离锥面。设细线与水平方向成γ角。
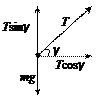 则有:
则有: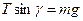

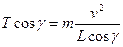
 可得:
可得: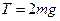

 垂直圆柱端面看:圆柱受力如图所示:两支持力N对称大小相等,且与重力Mg的垂直棱的分力Mgcos37°互成120°,则有:
垂直圆柱端面看:圆柱受力如图所示:两支持力N对称大小相等,且与重力Mg的垂直棱的分力Mgcos37°互成120°,则有:
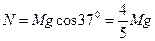
 由不滑动的条件有:
由不滑动的条件有: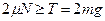
 所以:
所以: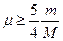


练习册系列答案
相关题目
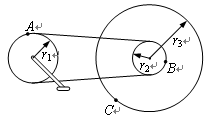

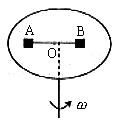
 ,离轴心
,离轴心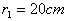 ,B的质量为
,B的质量为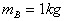 ,离轴心
,离轴心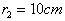 ,A、B与盘面间相互作用的摩擦力最大值为其重力的0.5倍,试求:
,A、B与盘面间相互作用的摩擦力最大值为其重力的0.5倍,试求: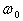 为多少时,细线上开始出现张力?
为多少时,细线上开始出现张力?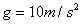 )
)
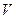 的超重车,行驶在半径为厅的圆弧形拱桥顶点,已知此处桥面能承受的最大压力只是车重的
的超重车,行驶在半径为厅的圆弧形拱桥顶点,已知此处桥面能承受的最大压力只是车重的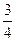 倍;要使车能安全沿桥面行驶,求在此处车的速度应在什么范围内?
倍;要使车能安全沿桥面行驶,求在此处车的速度应在什么范围内?