Question

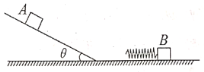
【题目】水平面上固定着倾角θ=37°的斜面，将质量m=lkg的物块A从斜面上无初速度释放，其加速度a=3m/s2。经过一段时间，物块A与静止在斜面上的质量M=2kg的物块B发生完全非弹性碰撞，之后一起沿斜面匀速下滑。已知重力加速度大小g=10m/s2，sin37°=0.6，co37°=0.8，求

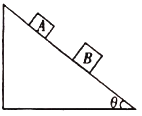
(1)A与斜面之间的动摩擦因数μ1；

(2)B与斜面之间的动摩擦因数μ2。

Answer 1

【答案】(1)() (2) ()

【解析】

物块A沿斜面加速下滑，由滑动摩擦力公式和力的平衡条件求解A与斜面之间的动摩擦因数；

A、B一起沿斜面下匀速下滑，以整体为研究对象，由滑动摩擦力公式和力的平衡条件求解B与斜面之间的动摩擦因数。

(1)物块A沿斜面加速下滑，

由滑动摩擦力公式和力的平衡条件得：

由牛顿第二定律得：

解得：；

(2)A、B一起沿斜面下匀速下滑，以整体为研究对象，由滑动摩擦力公式和力的平衡条件得：

解得：。