题目内容
（2005?南京一模）如图所示，在绕竖直轴匀速转动的水平圆盘盘面上，离轴心r=20cm处放置一小物块A，其质量为m=2kg，A与盘面间相互作用的静摩擦力的最大值为其重力的k倍（k=0.5），试求：（1）当圆盘转动的角速度ω=2rad/s时，物块与圆盘间的摩擦力大小多大？方向如何？
（2）欲使A与盘面间不发生相对滑动，则圆盘转动的最大角速度多大？（取g=10m/s2）
分析：（1）对滑块受力分析，受到重力、支持力和指向圆心的静摩擦力，合力提供向心力，根据牛顿第二定律列式求解即可；
（2）当静摩擦力达到最大值时，转动的加速度最大，根据静摩擦力提供向心力，运用牛顿第二定律列式求解即可．
（2）当静摩擦力达到最大值时，转动的加速度最大，根据静摩擦力提供向心力，运用牛顿第二定律列式求解即可．
解答：解：（1）f=mω2r=2×22×0.2N=1.6N…①
方向为指向圆心． …②
即当圆盘转动的角速度ω=2rad/s时，物块与圆盘间的摩擦力大小为1.6N，方向总是指向圆心．
（2）当最大静摩擦力提供向心力时，加速度最大，根据牛顿第二定律，有
kmg=mωm2r…③
解得
ωm=
=5rad/s…④
即圆盘转动的最大角速度为5rad/s．
方向为指向圆心． …②
即当圆盘转动的角速度ω=2rad/s时，物块与圆盘间的摩擦力大小为1.6N，方向总是指向圆心．
（2）当最大静摩擦力提供向心力时，加速度最大，根据牛顿第二定律，有
kmg=mωm2r…③
解得
ωm=
|
即圆盘转动的最大角速度为5rad/s．
点评：本题关键对物体受力分析，然后根据合力提供向心力，运用牛顿第二定律列式求解即可．
练习册系列答案
阅读快车系列答案
相关题目
（2005?南京一模）一束一价正离子流垂直于电场方向进入匀强电场，若它们飞出电场的偏向角相同（如图），则可断定它们进入电场时（ ）
（2005?南京二模）在研究性学习中，某同学设计了一个测定带电粒子比荷的实验，其实验装置如图所示．abcd是一个长方形盒子，在ad边和cd边上各开有小孔f和e，e是cd边上的中点，荧光屏M贴着cd放置，能显示从e孔射出的粒子落点位置．盒子内有一方向垂直于abcd平面的匀强磁场，磁感应强度大小为B．粒子源不断地发射相同的带电粒子，粒子的初速度可忽略．粒子经过电压为U的电场加速后，从f孔垂直于ad边射入盒内．粒子经磁场偏转后恰好从e孔射出．若已知fd=cd=L，不计粒子的重力和粒子之间的相互作用力．请你根据上述条件求出带电粒子的比荷q/m．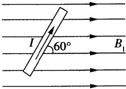
（2005?南京三模）如图所示，平行于纸面水平向右的匀强磁场，磁感应强度B1=1T．位于纸面内的细直导线，长L=1m，通有I=1A的恒定电流．当导线与B成60°夹角时，发现其受到的安培力为零．则该区域同时存在的另一匀强磁场的磁感应强度B2大小可能值（ ）