题目内容
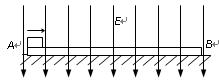
(18分)质量为m,长为L的矩形绝缘板放在光滑水平面上,另有一质量为m,带电量为q的小物块沿板的上表面以某一初速度从左端A水平向右滑上该板,整个装置处于竖直向下,足够大的匀强电场中,小物块沿板运动至右端B恰好停在板上.若强场大小不变而方向反向,当小物块仍由A端以相同的初速度滑上板面,则小物块运动到距A端的距离为板长2/3处时,就相对于板静止了。
(1)通过计算说明小物块带何种电荷?匀强电场场强的大小E是多少?
(2)撤去电场,在绝缘板上距A端为 处固定一质量可以忽略的挡板,小物块以相同初速度滑上绝缘板,与该挡板发生弹性正碰,求
处固定一质量可以忽略的挡板,小物块以相同初速度滑上绝缘板,与该挡板发生弹性正碰,求 至少多大时,小物块不会从绝缘板上掉下。
至少多大时,小物块不会从绝缘板上掉下。

【答案】
(1)负电荷;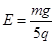
(2)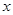 至少等于
至少等于 时,小物块不会掉下
时,小物块不会掉下
【解析】(1)由题意知:电场方向向下和向上时,两物体都达到了共同速度,设初速度为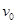 ,动摩擦因数为
,动摩擦因数为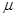 ,由动量守恒得
,由动量守恒得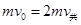 ……①
……2分
……①
……2分
由功能关系可知两次系统损失的机械能相同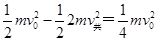 ……② …2分
……② …2分
而 …………③ …………2分
…………③ …………2分
E向下时,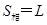 E向上时,
E向上时,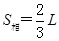

 …………④
………………2分
…………④
………………2分
而 正比于
正比于 即第一次正压力较小,第一次受到的电场力一定向上,
即第一次正压力较小,第一次受到的电场力一定向上,
由此可以判定小物块带负电荷, …………2分
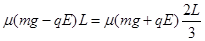
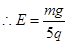 ……2分
……2分
(2)撤去电场后,发生了弹性正碰,碰撞无机械能损失,物块不掉下,最终达到共同速度,由动量守恒,功能关系得
 ………………⑤ ……1分
………………⑤ ……1分
 ……⑥ ……2分
……⑥ ……2分
 ……⑦ ……1分
……⑦ ……1分
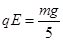 ……⑧ ……1分
……⑧ ……1分
联立⑤⑥⑦⑧得 
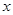 至少等于
至少等于 时,小物块不会掉下……1分
时,小物块不会掉下……1分

练习册系列答案
相关题目
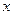 处固定一质量可以忽略的挡板,小物块以相同初速度滑上绝缘板,与该挡板发生弹性正碰,求
处固定一质量可以忽略的挡板,小物块以相同初速度滑上绝缘板,与该挡板发生弹性正碰,求