题目内容
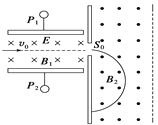
【题目】如图所示,在虚线HF上方存在着垂直于纸面向里的匀强磁场B1,在x轴上方存在沿x轴正方向的匀强电场,在x轴下方的矩形区域ABCD内还存在垂直于纸面向外的匀强磁场,矩形区域的AB边与x轴重合。M点是HF和y轴的交点,在M点有一静止镭核(![]() ),某时刻发生放射性衰变,放出某种质量为m、电荷量为q的粒子后变为一氡核(
),某时刻发生放射性衰变,放出某种质量为m、电荷量为q的粒子后变为一氡核(![]() ),氡核恰好沿y轴正向做匀速直线运动,粒子则以初速度v0沿y轴负方向运动,恰好从N点进入磁场,当粒子第二次经过x轴时电场反向,粒子恰好回到M点,若|OM|=2|ON|,核子的质量数与质量成正比,不计氡核和粒子的重力。
),氡核恰好沿y轴正向做匀速直线运动,粒子则以初速度v0沿y轴负方向运动,恰好从N点进入磁场,当粒子第二次经过x轴时电场反向,粒子恰好回到M点,若|OM|=2|ON|,核子的质量数与质量成正比,不计氡核和粒子的重力。

(1)写出上述过程中镭核的衰变方程。
(2)求电场强度的大小E。
(3)求N点的横坐标x。
(4)求矩形区域ABCD内匀强磁场的磁感应强度的大小B2及矩形区域的最小面积S。
【答案】(1)![]() (2)
(2) ![]() (3)
(3) ![]() (4)
(4) 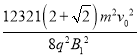
【解析】本题考查带电粒子的运动,需运用动量守恒、带电粒子在电场中的类平抛、带电粒子在磁场中的圆周运动等知识求解。
(1)镭衰变的核反应方程为![]()
(2)设氡核质量为m1,电荷量为q1,运动速度为v1,氡核恰好沿y轴正向做匀速直线运动根据力的平衡有: ![]()
镭核衰变时,根据动量守恒有: ![]()
其中![]()
解得: ![]()
(3)粒子从M点到N点做类平抛运动,设运动时间为t,O点到N点的距离为x,则
沿y轴负方向有: ![]()
沿x轴正方向有: ![]()
又有: ![]()
解得: ![]()
(4)粒子的运动轨迹如图所示
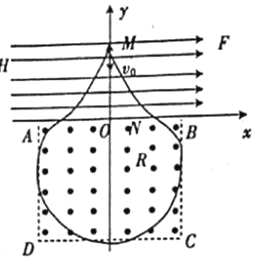
粒子经过N点时,在x轴方向有![]() ,解得:
,解得: ![]()
粒子进入磁场的速度![]()
设粒子进入磁场时速度方向与x轴方向的夹角为θ,因为![]()
所以θ=45°
由几何关系得粒子在磁场中做周运动的半径![]()
由牛顿第二定律得: ![]()
解得: ![]()
矩形区域的最小面积为![]()
解得: 

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目