题目内容
20. 如图所示,将劲度系数为k的轻弹簧竖直固定水平地面上.手持质量为m的物块从与弹簧接触(未连接)开始缓慢挤压弹簧.在弹性限度内弹簧长度被压缩了x,释放物块,物块开始向上运动,运动的最大距离为3x.不计空气阻力.重力加速度为g,则( )
如图所示,将劲度系数为k的轻弹簧竖直固定水平地面上.手持质量为m的物块从与弹簧接触(未连接)开始缓慢挤压弹簧.在弹性限度内弹簧长度被压缩了x,释放物块,物块开始向上运动,运动的最大距离为3x.不计空气阻力.重力加速度为g,则( )| A. | 释放瞬间,物体的加速度大小为$\frac{kx}{m}$ | |
| B. | 释放瞬间,弹簧的弹性势能大小为mgx | |
| C. | 物体从释放到最高点过程中,做匀减速运动的时间为$\sqrt{\frac{4x}{g}}$ | |
| D. | 物体从释放到最高点过程中,其中加速过程克服重力做的功为mgx |
分析 结合受力分析与牛顿第二定律即可求出加速度;由功能关系即可求出弹簧的弹性势能;物体在离开弹簧后才开始做匀减速运动;结合受力分析,确定加速过程物体上升的高度,即可求出加速过程克服重力做的功.
解答 解:A、弹性限度内弹簧长度被压缩了x,则弹簧的弹力大小为:F=kx,释放瞬间,物体受到重力和弹力的作用,加速度大小为:a=$\frac{F-mg}{m}$=$\frac{kx}{m}$-g.故A错误;
B、物体上升是最大距离是3x,则在最高点的重力势能为3mgx,由于上升的过程中弹簧的弹性势能转化为重力势能,所以可知,释放瞬间,弹簧的弹性势能大小为3mgx.故B错误;
C、物体在释放后,开始时受到重力和弹簧的弹力,随物体的上升,弹簧的弹力减小,所以物体做加速度减小化的加速运动;当弹簧的弹力小于重力后做减速运动,直到物体离开弹簧后只受到重力时,才开始做匀减速直线运动,所以做匀减速运动的距离在2x,运动的时间:$t=\sqrt{\frac{2h}{g}}=\sqrt{\frac{4x}{g}}$.故C正确;
D、物体在释放后,开始时受到重力和弹簧的弹力,随物体的上升,弹簧的弹力减小,所以物体做加速度减小化的加速运动;当弹簧的弹力小于重力后做减速运动,所以加速过程中的位移:$△x=x-\frac{mg}{k}$.该过程中克服重力做的功:$W=mg(x-\frac{mg}{k})$.故D错误.
故选:C
点评 解决本题的关键会通过物体的受力判断物体的运动,知道弹力和重力相等时,速度最大.理解好机械能守恒的条件是:只有重力或弹力做功,但是有弹力做功时是物体与弹簧组成的系统机械能守恒.

练习册系列答案
相关题目
10. 当汽车通过拱桥顶点的速度为10m/s时,车对桥顶的压力为车重的$\frac{3}{4}$,如果要使汽车能安全通过该拱形桥(不脱离地面),则汽车通过桥顶的速度可以为(g=10m/s2)( )
当汽车通过拱桥顶点的速度为10m/s时,车对桥顶的压力为车重的$\frac{3}{4}$,如果要使汽车能安全通过该拱形桥(不脱离地面),则汽车通过桥顶的速度可以为(g=10m/s2)( )
 当汽车通过拱桥顶点的速度为10m/s时,车对桥顶的压力为车重的$\frac{3}{4}$,如果要使汽车能安全通过该拱形桥(不脱离地面),则汽车通过桥顶的速度可以为(g=10m/s2)( )
当汽车通过拱桥顶点的速度为10m/s时,车对桥顶的压力为车重的$\frac{3}{4}$,如果要使汽车能安全通过该拱形桥(不脱离地面),则汽车通过桥顶的速度可以为(g=10m/s2)( )| A. | 15m/s | B. | 20m/s | C. | 23m/s | D. | 18m/s |
8.小球做匀速圆周运动过程中,不发生变化的物理量是( )
| A. | 线速度 | B. | 向心力 | C. | 加速度 | D. | 动能 |
5.下列说法中正确的是( )
| A. | 发射无线电波必须进行调制,接收电磁波必须进行调谐 | |
| B. | 处于基态的氢原子向源发态跃迁时,要吸收能量,跃迁后,动能变大 | |
| C. | 在不同惯性中测得光在真空中运动的速率可能不同 | |
| D. | 激光具有高亮度、单色性、相干性的优点,其应用有激光切割、全息照相等 |
12.两颗人造卫星A、B绕地球做匀速圆周运动,轨道半径之比为RA:RB=2:1,则向心加速度之比和运动速率之比分别为( )
| A. | aA:aB=1:4,VA:VB=$\sqrt{2}$:1 | B. | aA:aB=1:4,VA:VB=1:$\sqrt{2}$ | ||
| C. | aA:aB=4:1,VA:VB=$\sqrt{2}$:1 | D. | aA:aB=4:1,VA:VB=1:$\sqrt{2}$ |
10.下列实例中满足机械能守恒定律的是( )
| A. | 加速上升的气球 | |
| B. | 在空中匀速下落的树叶 | |
| C. | 斜向上抛出的铅球(不计空气阻力) | |
| D. | 在竖直平面内作匀速圆周运动的小球 |
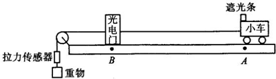 利用如图所示的实验装置以小车为对象来“探究合力做功与物体动能改变的关系”,将光电门固定在轨道上的B点,用重物通过细线拉小车,连线上安装一拉力传感器.已知小车质量为M,保持小车质量不变,改变所挂重物质量m多次进行实验,每次小车都从同一位置A由静止释放(g取10m/s2)
利用如图所示的实验装置以小车为对象来“探究合力做功与物体动能改变的关系”,将光电门固定在轨道上的B点,用重物通过细线拉小车,连线上安装一拉力传感器.已知小车质量为M,保持小车质量不变,改变所挂重物质量m多次进行实验,每次小车都从同一位置A由静止释放(g取10m/s2) 如图所示,光滑水平面上有一质量m=2kg的物体,在大小为5N、方向水平向右的拉力F作用下由静止开始运动.求:(g取10m/s2)
如图所示,光滑水平面上有一质量m=2kg的物体,在大小为5N、方向水平向右的拉力F作用下由静止开始运动.求:(g取10m/s2)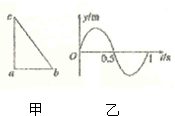 如图甲所示,在水平面内,有三个质点a、b、c分别位于直角三角形的三个顶点上,已知ab=6m,ac=8m,在t1=0时刻a、b同时开始振动,振动图象均如图乙所示,所形成的机械波在水平面内传播,在t2=4s时c点开始振动,则该机械波的传播速度大小为2m/s;两列波相遇后叠加,c点的振动加强(选填“加强”、“减弱”、“先加强后减弱”).
如图甲所示,在水平面内,有三个质点a、b、c分别位于直角三角形的三个顶点上,已知ab=6m,ac=8m,在t1=0时刻a、b同时开始振动,振动图象均如图乙所示,所形成的机械波在水平面内传播,在t2=4s时c点开始振动,则该机械波的传播速度大小为2m/s;两列波相遇后叠加,c点的振动加强(选填“加强”、“减弱”、“先加强后减弱”).