题目内容
10. 当汽车通过拱桥顶点的速度为10m/s时,车对桥顶的压力为车重的$\frac{3}{4}$,如果要使汽车能安全通过该拱形桥(不脱离地面),则汽车通过桥顶的速度可以为(g=10m/s2)( )
当汽车通过拱桥顶点的速度为10m/s时,车对桥顶的压力为车重的$\frac{3}{4}$,如果要使汽车能安全通过该拱形桥(不脱离地面),则汽车通过桥顶的速度可以为(g=10m/s2)( )| A. | 15m/s | B. | 20m/s | C. | 23m/s | D. | 18m/s |
分析 根据竖直方向上的合力提供向心力求出桥的半径,当汽车不受摩擦力时,支持力为零,则靠重力提供向心力,根据牛顿第二定律求出汽车通过桥顶的速度
解答 解:根据牛顿第二定律得:mg-N=m$\frac{{v}^{2}}{r}$,
即:mg-$\frac{3}{4}$mg=m$\frac{{v}^{2}}{r}$
解得:r=$\frac{4{v}^{2}}{g}$=40m;
当摩擦力为零时,支持力为零,有:mg=m$\frac{v{′}^{2}}{r}$,
解得:v′=$\sqrt{gr}$=2v=20m/s.
则汽车通过桥顶的速度可以为<20m/s即可,
故A、D正确,B、C错误.
故选:AD.
点评 解决本题的关键知道圆周运动向心力的来源,运用牛顿第二定律进行求解.知道摩擦力为零时,此时支持力为零.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
15.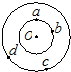 如图所示,两个等量异种点电荷对称地放在一无限大平面的两侧(两点电荷未画出),O点是两点电荷连线与平面的交点,也是连线的中点.在平面内以O点为圆心画两个同心圆,两圆上分别有a、b、c、d四个点,则以下说法正确的是( )
如图所示,两个等量异种点电荷对称地放在一无限大平面的两侧(两点电荷未画出),O点是两点电荷连线与平面的交点,也是连线的中点.在平面内以O点为圆心画两个同心圆,两圆上分别有a、b、c、d四个点,则以下说法正确的是( )
 如图所示,两个等量异种点电荷对称地放在一无限大平面的两侧(两点电荷未画出),O点是两点电荷连线与平面的交点,也是连线的中点.在平面内以O点为圆心画两个同心圆,两圆上分别有a、b、c、d四个点,则以下说法正确的是( )
如图所示,两个等量异种点电荷对称地放在一无限大平面的两侧(两点电荷未画出),O点是两点电荷连线与平面的交点,也是连线的中点.在平面内以O点为圆心画两个同心圆,两圆上分别有a、b、c、d四个点,则以下说法正确的是( )| A. | a、c两点电场强度大小相等 | |
| B. | 若某个检验电荷只在此电场的电场力作用下运动到c点和d点时,加速度大小一定相等 | |
| C. | 带正电的检验电荷从a点在平面内移动到d点电势能一定不变 | |
| D. | 检验电荷可以仅在此电场的电场力作用下在此平面内做匀速圆周运动 |
2.以下说法错误的是( )
| A. | 卫星越往高的地方发射所需要的速度越大,但越高的卫星运行速度越慢 | |
| B. | 同一位置方向上,以较大速度发射卫星所得到的最终运行速度比以较小速度发射所得到的大 | |
| C. | 越高处的卫星速度越慢,因此可以通过加速来降低高度 | |
| D. | 以第三宇宙速度发射,卫星也能逃离地球的引力 |
19.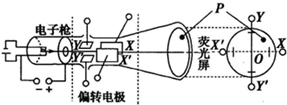 如图所示,示波管是示波器的核心部件,它由电子枪、偏转电极和荧光屏组成.如果在荧光屏上P点出现亮斑,那么示波管中的( )
如图所示,示波管是示波器的核心部件,它由电子枪、偏转电极和荧光屏组成.如果在荧光屏上P点出现亮斑,那么示波管中的( )
 如图所示,示波管是示波器的核心部件,它由电子枪、偏转电极和荧光屏组成.如果在荧光屏上P点出现亮斑,那么示波管中的( )
如图所示,示波管是示波器的核心部件,它由电子枪、偏转电极和荧光屏组成.如果在荧光屏上P点出现亮斑,那么示波管中的( )| A. | 极板X应带正电 | B. | 极板X′应带正电 | C. | 极板Y应带负电 | D. | 极板Y′应带负电 |
20. 如图所示,将劲度系数为k的轻弹簧竖直固定水平地面上.手持质量为m的物块从与弹簧接触(未连接)开始缓慢挤压弹簧.在弹性限度内弹簧长度被压缩了x,释放物块,物块开始向上运动,运动的最大距离为3x.不计空气阻力.重力加速度为g,则( )
如图所示,将劲度系数为k的轻弹簧竖直固定水平地面上.手持质量为m的物块从与弹簧接触(未连接)开始缓慢挤压弹簧.在弹性限度内弹簧长度被压缩了x,释放物块,物块开始向上运动,运动的最大距离为3x.不计空气阻力.重力加速度为g,则( )
 如图所示,将劲度系数为k的轻弹簧竖直固定水平地面上.手持质量为m的物块从与弹簧接触(未连接)开始缓慢挤压弹簧.在弹性限度内弹簧长度被压缩了x,释放物块,物块开始向上运动,运动的最大距离为3x.不计空气阻力.重力加速度为g,则( )
如图所示,将劲度系数为k的轻弹簧竖直固定水平地面上.手持质量为m的物块从与弹簧接触(未连接)开始缓慢挤压弹簧.在弹性限度内弹簧长度被压缩了x,释放物块,物块开始向上运动,运动的最大距离为3x.不计空气阻力.重力加速度为g,则( )| A. | 释放瞬间,物体的加速度大小为$\frac{kx}{m}$ | |
| B. | 释放瞬间,弹簧的弹性势能大小为mgx | |
| C. | 物体从释放到最高点过程中,做匀减速运动的时间为$\sqrt{\frac{4x}{g}}$ | |
| D. | 物体从释放到最高点过程中,其中加速过程克服重力做的功为mgx |
 如图所示,一光滑小球在水平面上沿直线从a匀速运动到b点,空气阻力不计.当小球运动到b点时受到水平面内垂直于ab连线方向的快速一击,这之后小球运动的轨迹可能是图中的( )
如图所示,一光滑小球在水平面上沿直线从a匀速运动到b点,空气阻力不计.当小球运动到b点时受到水平面内垂直于ab连线方向的快速一击,这之后小球运动的轨迹可能是图中的( )



 如图所示,竖直向下磁感强度B=1T的匀强磁场中,水平放置了间距宽度为0.6m的U形光滑轨道,导轨左端连接了阻值R=1Ω的电阻和开关,一根阻值r=3Ω的导体棒ab放在U形轨道上,其中$\frac{1}{3}$在轨道以外.
如图所示,竖直向下磁感强度B=1T的匀强磁场中,水平放置了间距宽度为0.6m的U形光滑轨道,导轨左端连接了阻值R=1Ω的电阻和开关,一根阻值r=3Ω的导体棒ab放在U形轨道上,其中$\frac{1}{3}$在轨道以外.