题目内容
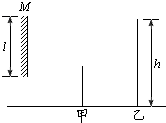 图中M是竖直放置的平面镜,镜离地面的距离可调节.甲、乙二人站在镜前,乙离镜的距离为甲离镜的距离的2倍,如图所示.二人略错开,以便甲能看到乙的像.以l表示镜的长度,h表示乙的身高,为使甲能看到镜中乙的全身像,l的最小值为( )
图中M是竖直放置的平面镜,镜离地面的距离可调节.甲、乙二人站在镜前,乙离镜的距离为甲离镜的距离的2倍,如图所示.二人略错开,以便甲能看到乙的像.以l表示镜的长度,h表示乙的身高,为使甲能看到镜中乙的全身像,l的最小值为( )分析:本题为平面镜成像问题,人眼能看到完整的像应让两端的光线经反射后进入眼睛;再由作图法找出能看到全身像的l长度的最小值.
解答: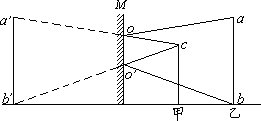 解:采用物像对应(虚线a′b′是乙ab的像)和边缘光线(c是甲的眼睛,aoc与bo′c是边缘光如线)作出甲能看到乙的像的光路图所示,则oo′为甲能看到镜中乙的全身像所需的最小镜面.在三角形ca′b′中根据相似性可得,oo′是ab的三分之一.
解:采用物像对应(虚线a′b′是乙ab的像)和边缘光线(c是甲的眼睛,aoc与bo′c是边缘光如线)作出甲能看到乙的像的光路图所示,则oo′为甲能看到镜中乙的全身像所需的最小镜面.在三角形ca′b′中根据相似性可得,oo′是ab的三分之一.
故选A.
 解:采用物像对应(虚线a′b′是乙ab的像)和边缘光线(c是甲的眼睛,aoc与bo′c是边缘光如线)作出甲能看到乙的像的光路图所示,则oo′为甲能看到镜中乙的全身像所需的最小镜面.在三角形ca′b′中根据相似性可得,oo′是ab的三分之一.
解:采用物像对应(虚线a′b′是乙ab的像)和边缘光线(c是甲的眼睛,aoc与bo′c是边缘光如线)作出甲能看到乙的像的光路图所示,则oo′为甲能看到镜中乙的全身像所需的最小镜面.在三角形ca′b′中根据相似性可得,oo′是ab的三分之一.故选A.
点评:平面镜成像关键在于根据物像对称原理可以得出完整的像,再结合人眼的位置即可做出的需光路图.本题也可做出甲的眼镜的像来解答.

练习册系列答案
相关题目
如图所示,M、N是竖直放置的两平行金属板,分别带等量异种电荷,两极间产生一个水平向右的匀强电场,场强为E,一质量为m、电量为+q的微粒,以初速度v0竖直向上从两极正中间的A点射入匀强电场中,微粒垂直打到N极上的C点,已知AB=BC.不计空气阻力,则可知( )
| A.微粒在电场中作类平抛运动 |
| B.微粒打到C点时的速率与射入电场时的速率相等 |
C.MN板间的电势差为2mv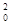 /q /q |
D.MN板间的电势差为Ev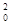 /2g /2g |
 如图所示,M、N是竖直放置的两平行金属板,分别带等量异种电荷,两极间产生一个水平向右的匀强电场,场强为E,一质量为m、电荷量为+q的微粒,以初速度v0竖直向上从两极正中间的A点射入匀强电场中,微粒垂直打到N极上的C点,已知AB=BC.不计空气阻力,则可知( )
如图所示,M、N是竖直放置的两平行金属板,分别带等量异种电荷,两极间产生一个水平向右的匀强电场,场强为E,一质量为m、电荷量为+q的微粒,以初速度v0竖直向上从两极正中间的A点射入匀强电场中,微粒垂直打到N极上的C点,已知AB=BC.不计空气阻力,则可知( )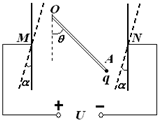 如图所示,竖直放置的两平行带电金属板间的匀强电场中有一根质量为m的均匀绝缘杆,上端可绕轴O在竖直平面内转动,下端固定一个不计重力的点电荷A,带电量+q.当板间电压为U1时,杆静止在与竖直方向成θ=45°的位置;若平行板以M、N为轴同时顺时针旋转α=15°的角,而仍要杆静止在原位置上,则板间电压应变为U2.求:U1/U2的比值.
如图所示,竖直放置的两平行带电金属板间的匀强电场中有一根质量为m的均匀绝缘杆,上端可绕轴O在竖直平面内转动,下端固定一个不计重力的点电荷A,带电量+q.当板间电压为U1时,杆静止在与竖直方向成θ=45°的位置;若平行板以M、N为轴同时顺时针旋转α=15°的角,而仍要杆静止在原位置上,则板间电压应变为U2.求:U1/U2的比值. =45°的位置;若平行板以M、N为轴同时顺时针旋转
=45°的位置;若平行板以M、N为轴同时顺时针旋转 =15°的角,而仍要杆静止在原位置上,则板间电压应变为U2。求:U1/U2的比值。
=15°的角,而仍要杆静止在原位置上,则板间电压应变为U2。求:U1/U2的比值。
 变为
变为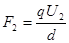 ,电场力对轴O的力臂也发生相应的改变,但电场力对轴O的力矩没有改变。只要列出两种情况下的力矩平衡方程,就可求解了。
,电场力对轴O的力臂也发生相应的改变,但电场力对轴O的力矩没有改变。只要列出两种情况下的力矩平衡方程,就可求解了。 =45°的位置;若平行板以M、N为轴同时顺时针旋转
=45°的位置;若平行板以M、N为轴同时顺时针旋转 =15°的角,而仍要杆静止在原位置上,则板间电压应变为U2。求:U1/U2的比值。
=15°的角,而仍要杆静止在原位置上,则板间电压应变为U2。求:U1/U2的比值。
 变为
变为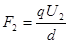 ,电场力对轴O的力臂也发生相应的改变,但电场力对轴O的力矩没有改变。只要列出两种情况下的力矩平衡方程,就可求解了。
,电场力对轴O的力臂也发生相应的改变,但电场力对轴O的力矩没有改变。只要列出两种情况下的力矩平衡方程,就可求解了。