题目内容
【题目】如图甲所示，竖直平面内的光滑轨道由倾斜直轨道AB和圆轨道BCD组成，AB和BCD相切于B点，CD连线是圆轨道竖直方向的直径（C，D为圆轨道的最低点和最高点），且∠BOC=θ=37°，圆轨道直径d为0.4m．可视为质点质量m为0.1kg的小滑块从轨道AB上高H处的某点由静止滑下，（已知sin37°=0.6，cos37°=0.8）：求
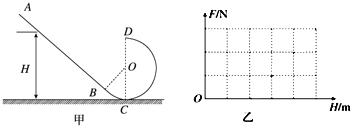
（1）小滑块从某处静止开始下滑，求刚好能通过圆轨道最高点D的高度H；
（2）若用力传感器测出滑块经过圆轨道最高点D时对轨道的压力为F，请在如图乙中绘制出压力F与高度H的关系图象．
（3）通过计算判断是否存在某个H值，使得滑块经过最高点D后能直接落到直轨道AB上与圆心等高的点．
【答案】(1)0.5m；(2)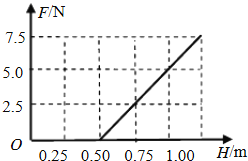 
；(3)存在满足条件的
值
【解析】
解：(1)刚好通过圆轨道最高点
时，由牛顿第二定律得：
由机械能守恒定律得：
联立解得：
(2)滑块由从某高度处下滑到的过程中，由机械能守恒定律得：
由牛顿第三定律得滑块在点所受轨道支持力与滑块对轨道的压力等大反向，记为
，则由牛顿第二定律得：
代入数据解得：
其图象如图所示
(3)存在满足条件的值，设滑块在点的速度为
时，恰能落到直轨道上与圆心等高处
竖直方向：
，水平方向：
由几何关系得：
代入数据解得：
物体恰好能过点的速度大小：
因为
，所以存在满足条件的值
练习册系列答案
相关题目
