题目内容
14. 如图所示,物体M在某种毛皮的斜面上运动,该毛皮表面的特殊性使其具有如下特点:
如图所示,物体M在某种毛皮的斜面上运动,该毛皮表面的特殊性使其具有如下特点:①毛皮上的物体顺着毛的生长方向运动时,毛皮产生的阻力可以忽略;②毛皮上的物体逆着毛的生长方向运动会受到来自毛皮的滑动摩擦力,且动摩擦因数μ=0.5.斜面頂端距水平面的高度h=0.8m,质量为m=2kg的小物块M从斜面顶端A有静止滑下.逆着毛的生长方向运动到斜面底端的0点进入光滑水平滑道(忽略从斜面进入水平面过程中小物块机械能的损失).为使M制动,将轻弹簧的一端固定在水平滑道延长线B处的竖直墙上,另一端位于水平轨进的C点,己知弹簧始终处于弹性限度内,斜面的倾角θ=53°,重力加速度g=1Om/s2,sin53°=0.8,cos53°=0.6,求:
(1)小物块第一次从A运动到O过程中克服摩擦力做的功;
(1)小物块第一次到达0点的速度大小;
(2)从开始运动到最终静止的过程中,小物块在斜面上通过的总路程.
分析 (1)小物块第一次从A运动到O过程中,根据W=FLcosθ求的下滑过程克服摩擦力做功即可;
(2)根据动能定理求小物块第一次到达0点的速度大小;
(3)物体最终静止在地面上,对全过程,根据动能定理求出总路程.
解答 解:(1)小物块第一次从A运动到O过程中克服摩擦力做的功为:
Wf=μmgcos53°•$\frac{h}{sin53°}$=μmghcot53°=0.5×20×0.8×$\frac{3}{4}$J=6J
(2)物块第一次下滑过程,根据动能定理可得:
mgh-Wf=$\frac{1}{2}$mv2-0
解得:v=$\sqrt{\frac{2(mgh-{W}_{f})}{m}}$=$\sqrt{\frac{2×(20×0.8-6)}{2}}$=$\sqrt{10}$m/s
(3)物体最终静止在地面上,由动能定理可得:
mgh-μmgScos53°=0-0
代入数据解得:S=$\frac{8}{3}$m
故小物块在斜面上通过的总路程为:S总=2S=$\frac{16}{3}$m
答:(1)小物块第一次从A运动到O过程中克服摩擦力做的功是6J;
(1)小物块第一次到达0点的速度大小是$\sqrt{10}$m/s;
(2)从开始运动到最终静止的过程中,小物块在斜面上通过的总路程是$\frac{16}{3}$m.
点评 本题主要考查了动能定理,能灵活选择研究的过程,采用分段法和全程法结合研究,要注意滑动摩擦力做功与总路程有关.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.下列说法中正确的是( )
| A. | 在空中将物体释放后,物体不受重力作用 | |
| B. | 物体向上运动时所受的重力比向下运动时所受的重力大 | |
| C. | 物体重心的位置与物体的形状无关 | |
| D. | 在地球上方的物体都要受到重力作用,不管是否存在其他力的作用 |
16.物体做匀加速直线运动,已知第1s内的平均速度是5m/s,第2s末的速度是8m/s,则下面结论正确的是( )
| A. | 物体零时刻的速度是2 m/s | B. | 物体的加速度是2 m/s2 | ||
| C. | 任何1 s内的速度变化都是2 m/s | D. | 第3 s内的位移等于10m |
2. 如图所示,电源电动势为E,内阻为r,电压表、电流表均为理想电表,电键闭合后,小灯泡均能发光,在将滑动变阻器的触片逐渐向左滑动的过程中,下列说法正确的是( )
如图所示,电源电动势为E,内阻为r,电压表、电流表均为理想电表,电键闭合后,小灯泡均能发光,在将滑动变阻器的触片逐渐向左滑动的过程中,下列说法正确的是( )
 如图所示,电源电动势为E,内阻为r,电压表、电流表均为理想电表,电键闭合后,小灯泡均能发光,在将滑动变阻器的触片逐渐向左滑动的过程中,下列说法正确的是( )
如图所示,电源电动势为E,内阻为r,电压表、电流表均为理想电表,电键闭合后,小灯泡均能发光,在将滑动变阻器的触片逐渐向左滑动的过程中,下列说法正确的是( )| A. | 电压表V的读数变大 | B. | 电流表A的读数变小 | ||
| C. | 小灯泡L1、L2均变亮,L3变暗 | D. | 小灯泡L1、L3均变亮,L2变暗 |
19.某同学选用如图1所示的装置做“测定匀变速直线运动的加速度”的实验,电源的频率为50Hz.
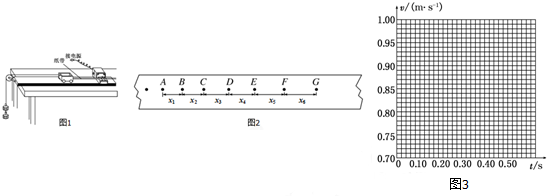
(1)该同学根据打出的纸带认为不用计算就能直接得到的物理量有两个,请帮他选出AB
A、时间间隔 B、位移 C、加速度 D、平均速度
(2)该同学选出了一条的清晰纸带,并根据纸带上的点,标出了如图2所示的计数点,其中两相邻计数点间还有4个点未画出,x1=7.05cm,x2=7.68cm,x3=8.33cm,x4=8.95cm,x5=9.61cm,x6=10.26cm.上表列出了打点计时器打下B、C、F时小车的瞬时速度,请在表中填入打点计时器打下D、E两点时小车的瞬时速度.
(4)根据(3)问的数据,以A点为计时起点,在图3中画出小车的速度-时间关系图线,并利用图象求出小车的加速度大小为0.64m/s2.

(1)该同学根据打出的纸带认为不用计算就能直接得到的物理量有两个,请帮他选出AB
A、时间间隔 B、位移 C、加速度 D、平均速度
(2)该同学选出了一条的清晰纸带,并根据纸带上的点,标出了如图2所示的计数点,其中两相邻计数点间还有4个点未画出,x1=7.05cm,x2=7.68cm,x3=8.33cm,x4=8.95cm,x5=9.61cm,x6=10.26cm.上表列出了打点计时器打下B、C、F时小车的瞬时速度,请在表中填入打点计时器打下D、E两点时小车的瞬时速度.
| 位置 | B | C | D | E | F |
| 速度(m/s) | 0.737 | 0.801 | 0.994 |
6.在电场强度大小为E的匀强电场中,将一个质量为m、带电量为q的小球由静止开始释放,带电小球沿与竖直方向成θ角做直线运动.关于带电小球的电势能Ep和机械能E机的判断正确的说法是( )
| A. | 若θ<90°且sinθ=$\frac{qE}{mg}$,则Ep、E机一定不变 | |
| B. | 若45°<θ<90°且tanθ=$\frac{qE}{mg}$,则Ep一定减小、E机一定增加 | |
| C. | 若0<θ<45°且tanθ=$\frac{qE}{mg}$,则Ep一定减小、E机一定增加 | |
| D. | 若0<θ<45°且tanθ=$\frac{qE}{mg}$,则Ep可能减少、E机可能增加 |
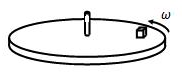 如图所示,在以角速度ω=2rad/s匀速转动的水平圆盘上,放一质量m=5kg的滑块,滑块离转轴的距离r=0.2m,滑块随圆盘一起做匀速圆周运动(二者未发生相对滑动).取g=10m/s2.
如图所示,在以角速度ω=2rad/s匀速转动的水平圆盘上,放一质量m=5kg的滑块,滑块离转轴的距离r=0.2m,滑块随圆盘一起做匀速圆周运动(二者未发生相对滑动).取g=10m/s2. 在“探究平抛运动规律”的实验中,可以描绘出小球平抛运动的轨迹,实验简要步骤如下:
在“探究平抛运动规律”的实验中,可以描绘出小球平抛运动的轨迹,实验简要步骤如下: