题目内容
(07年全国卷Ⅱ)(16分) 如图所示,位于竖直平面内的光滑轨道,由一段斜的直轨道的与之相切的圆形轨道连接而成,圆形轨道的半径为R。一质量为m的小物块从斜轨道上某处由静止开始下滑,然后沿圆形轨道运动。要求物块能通过圆形轨道的最高点,且在该最高点与轨道间的压力不能超过5mg(g为重力加速度)。求物块初始位置相对于圆形轨道底部的高度h的取值范围。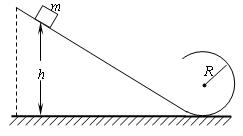
答案: ![]() R≤h≤5R
R≤h≤5R
解析:设物块在圆形轨道最高点的速度为v,由机械能守恒得
mgh=2mgR+![]() mv2 ①
mv2 ①
物块在最高点受的力为重力mg、轨道的压力N。重力与压力的合力提供向心力,有
mg+N=m![]() ②
②
物块能通过最高点的条件是
N>0 ③
由②③式得
v≥![]() ④
④
由①④式得
h≥![]() R ⑤
R ⑤
按题的要求,N≤5mg,由②⑤式得
v≤![]() ⑥
⑥
由①⑥式得
h≤5R ⑦
h的取值范围是
![]() R≤h≤5R
R≤h≤5R

 阅读快车系列答案
阅读快车系列答案(07年全国卷Ⅰ)如图所示,在倾角为30°的足够长的斜面上有一质量为m 的物体,它受到沿斜面方向 的力F的作用。力F可按图(a)、(b)、(c)、(d)所示的四种方式随时间变化(图中纵坐标是F与mg的比值,力沿斜面向上为正)。
的力F的作用。力F可按图(a)、(b)、(c)、(d)所示的四种方式随时间变化(图中纵坐标是F与mg的比值,力沿斜面向上为正)。
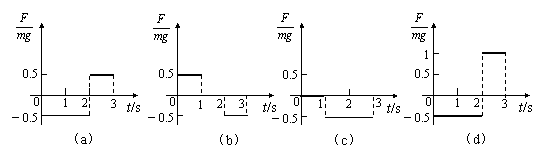 |
已知此物体在t=0时速度为零,若用v1、v2、v3、v4 分别表示上述四种受力情况下物体在3 s末的速率,则这四个速率中最大的是
A.v1 B.v2 C.v3 D.v4
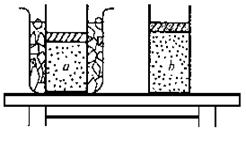 (07年全国卷Ⅰ)如图所示,质量为m的活塞将一定质量的气体封闭在气缸内,活塞与气缸之间无摩擦,a态是气缸放在冰水混合物中气体达到的平衡状态,b态是气缸从容器中移出后,在室温(27℃)中达到的平衡状态,气体从a态变化到b态的过程中大气压强保持不变。若忽略气体分子之间的势能,下列说法中正确的是
(07年全国卷Ⅰ)如图所示,质量为m的活塞将一定质量的气体封闭在气缸内,活塞与气缸之间无摩擦,a态是气缸放在冰水混合物中气体达到的平衡状态,b态是气缸从容器中移出后,在室温(27℃)中达到的平衡状态,气体从a态变化到b态的过程中大气压强保持不变。若忽略气体分子之间的势能,下列说法中正确的是 从桌面上有一倒立的玻璃圆锥,其顶点恰好与桌面接触,圆锥的轴(图中虚线)与桌面垂直,过轴线的截面为等边三角形,如图所示,有一半径为r的圆柱形平行光束垂直入射到圆锥的底面上,光束的中心轴与圆锥的轴重合。已知玻璃的折射率为1.5,则光束在桌面上形成的光斑半径为
从桌面上有一倒立的玻璃圆锥,其顶点恰好与桌面接触,圆锥的轴(图中虚线)与桌面垂直,过轴线的截面为等边三角形,如图所示,有一半径为r的圆柱形平行光束垂直入射到圆锥的底面上,光束的中心轴与圆锥的轴重合。已知玻璃的折射率为1.5,则光束在桌面上形成的光斑半径为 用大量具有一定能量的电子轰击大量处于基态的氢原子,观测到了一定数目的光谱线。调高电子的能量再次进行观测,发现光谱线的数目原来增加了5条。用△n表示两次观测中最高激发态的量子数n之差,E表示调高后电子的能量。根据氢原子的能级图可以判断,△n和E的可能值为
用大量具有一定能量的电子轰击大量处于基态的氢原子,观测到了一定数目的光谱线。调高电子的能量再次进行观测,发现光谱线的数目原来增加了5条。用△n表示两次观测中最高激发态的量子数n之差,E表示调高后电子的能量。根据氢原子的能级图可以判断,△n和E的可能值为 的四个顶点,电场线与矩形所在平面平行。已知a点的电势为20 V,b点的电势为24 V,d点的电势为4 V,如图,由此可知c点的电势为
的四个顶点,电场线与矩形所在平面平行。已知a点的电势为20 V,b点的电势为24 V,d点的电势为4 V,如图,由此可知c点的电势为