题目内容
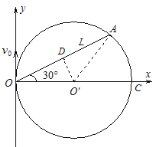
【题目】如图，在光滑水平面上建立平面直角坐标系xOy，第Ⅰ象限存在垂直于水平面的匀强磁场（图中未画出），一质量为m、电荷量为q的小球由坐标原点O处以速度v0沿y轴正方向射入磁场，一段时间后，小球与静止于A点的质量也为m但不带电的另一小球发生碰撞，并粘为一体，A点与原点O相距L，OA与x轴正方向的夹角为30°。
(1)求磁感应强度B的大小；
(2)两球碰撞后是否仍沿原来的的轨迹运动？试论证；
(3)求小球从O点射出到离开磁场所经历的时间t。
【答案】（1）
；（2）是，见解析；（3）
。
【解析】
（1）小球在磁场中做匀速圆周运动的轨迹如图所示，由几何关系得，小球做匀速圆周运动的半径为
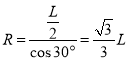
由牛顿第二定律得
解得，磁感应强度为
（2）两球碰撞过程遵循动量守恒定律
碰撞后两球继续做圆周运动，由
可得半径
两球碰撞后仍沿原来的的轨迹运动，只是速度变小，为原来的
。
（3）由几何关系可知
，小球从O点运动到A点的时间为
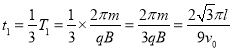
碰撞后，两球在磁场中运动的周期为
碰撞后两球在磁场里运动的时间
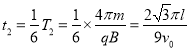
小球从O点射出到离开磁场所经历的时间
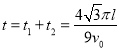
练习册系列答案
相关题目
