题目内容
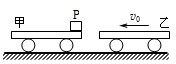
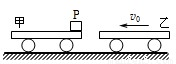
在光滑的水平面上原来停放着一辆质量为M1=2kg的平板小车甲,它的平板是光滑的,其右端放着一个质量为m=1kg的物块P(可视为质点),另一质量为M 2=4kg的平板小车乙以v=5m/s的速度向左运动,并跟甲车发生碰撞,如图所示,碰后甲车以6m/s的速度向左运动,物体P滑到乙车上.已知物体P跟乙车平板间的动摩擦因数为μ=0.2.求:(1)P在乙车上停止时,乙车的速度是多大?
(2)P在乙车上滑行的距离是多大?(设乙车平板足够长,g取10m/s2 )
【答案】分析:(1)对甲、乙以及P组成的系统,动量守恒,P在乙车上静止时,P与乙速度相等,根据系统动量守恒求出乙车的速度.
(2)在碰撞的瞬间,甲乙两车组成的系统动量守恒,根据动量守恒定律求出P刚滑上乙车时乙车的速度,再根对乙车和P分析,运用能量守恒定律求出P在乙车上滑行的距离.
解答:解:(1)通过碰撞最后P相对乙静止,即达到共同速度v3,由动量守恒定律得:
M2v=M1v1+(M2+m)v3
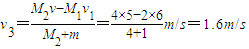 .
.
(2)两车相碰时P没有参与,所以两车动量守恒,设碰后乙车速度为v2,则
M2v=M1v1+M2v2
v2=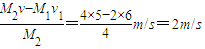
设P在乙车上滑行距离为L,根据功能关系有:μmgL=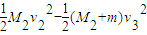
L=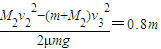 .
.
答:(1)P在乙车上停止时,乙车的速度是1.6m/s.
(2)P在乙车上滑行的距离是0.8m.
点评:本题综合考查了动量守恒定律和能量守恒定律,对学生能力的要求较高,关键是选择好系统,判断动量是否守恒,以及选择好研究的过程,运用合适的定律进行求解.
(2)在碰撞的瞬间,甲乙两车组成的系统动量守恒,根据动量守恒定律求出P刚滑上乙车时乙车的速度,再根对乙车和P分析,运用能量守恒定律求出P在乙车上滑行的距离.
解答:解:(1)通过碰撞最后P相对乙静止,即达到共同速度v3,由动量守恒定律得:
M2v=M1v1+(M2+m)v3
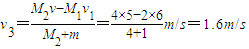 .
.(2)两车相碰时P没有参与,所以两车动量守恒,设碰后乙车速度为v2,则
M2v=M1v1+M2v2
v2=
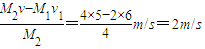
设P在乙车上滑行距离为L,根据功能关系有:μmgL=
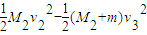
L=
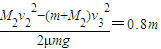 .
.答:(1)P在乙车上停止时,乙车的速度是1.6m/s.
(2)P在乙车上滑行的距离是0.8m.
点评:本题综合考查了动量守恒定律和能量守恒定律,对学生能力的要求较高,关键是选择好系统,判断动量是否守恒,以及选择好研究的过程,运用合适的定律进行求解.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 在光滑的水平面上原来停放着一辆质量为M1=2kg的平板小车甲,它的平板是光滑的,其右端放着一个质量为m=1kg的物块P(可视为质点),另一质量为M 2=4kg的平板小车乙以v0=5m/s的速度向左运动,并跟甲车发生碰撞,如图所示,碰后甲车以6m/s的速度向左运动,物体P滑到乙车上.已知物体P跟乙车平板间的动摩擦因数为μ=0.2.求:
在光滑的水平面上原来停放着一辆质量为M1=2kg的平板小车甲,它的平板是光滑的,其右端放着一个质量为m=1kg的物块P(可视为质点),另一质量为M 2=4kg的平板小车乙以v0=5m/s的速度向左运动,并跟甲车发生碰撞,如图所示,碰后甲车以6m/s的速度向左运动,物体P滑到乙车上.已知物体P跟乙车平板间的动摩擦因数为μ=0.2.求: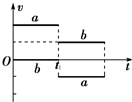 [物理--选修3-5]
[物理--选修3-5]