题目内容
【题目】将一个半球体置于水平地面上,半球的中央有一光滑小孔,上端有一光滑的小滑轮,柔软光滑的轻绳绕过滑轮,两端分别系有质量为![]() 、
、![]() 的物体(两物体均可看成质点,
的物体(两物体均可看成质点,![]() 悬于空中)时,整个装置处于静止状态,如图所示。已知此时
悬于空中)时,整个装置处于静止状态,如图所示。已知此时![]() 与半球的球心O的连线与水平线成
与半球的球心O的连线与水平线成![]() 角(sin
角(sin![]() =0.6,cos
=0.6,cos![]() =0.8),
=0.8),![]() 与半球面的动摩擦因数为0.5,并假设
与半球面的动摩擦因数为0.5,并假设![]() 所受到的最大静摩擦力等于滑动摩擦力。则在整个装置处于静止的前提下,下列说法正确的是( )
所受到的最大静摩擦力等于滑动摩擦力。则在整个装置处于静止的前提下,下列说法正确的是( )

A. 无论![]() 的比值如何,地面对半球体的摩擦力都为零
的比值如何,地面对半球体的摩擦力都为零
B. 当![]() 时,半球体对
时,半球体对![]() 的摩擦力为零,但对地面的摩擦力不为零
的摩擦力为零,但对地面的摩擦力不为零
C. 当![]()
![]()
![]()
![]() 时,
时,![]() 对半球体的摩擦力的方向垂直于图中的虚线向下
对半球体的摩擦力的方向垂直于图中的虚线向下
D. 当![]()
![]()
![]() ≤2时,半球体对
≤2时,半球体对![]() 的摩擦力的方向垂直于图中的虚线向上
的摩擦力的方向垂直于图中的虚线向上
【答案】AD
【解析】
A.对半球体m1、m2整体受力分析,只受重力和支持力这一对平衡力,相对地面并无运动趋势,故不受摩擦力,故A项正确;
B.若半球体对m1的摩擦力为零,对m1受力分析,如图
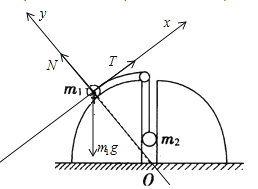
将重力正交分解,根据共点力平衡条件得到,x方向
![]()
y方向
![]()
据题意
![]()
解得:
![]()
对地面的摩擦力也为零,故B项错误;
C.当![]()
![]() <
<![]() 时,有
时,有![]() ,即拉力大于重力的下滑分量,m1有上滑趋势,m1摩擦力沿切线向下,
,即拉力大于重力的下滑分量,m1有上滑趋势,m1摩擦力沿切线向下,![]() 对半球体的摩擦力的方向垂直于图中的虚线向上,故C项错误;
对半球体的摩擦力的方向垂直于图中的虚线向上,故C项错误;
D.当![]() 时,有
时,有
![]()
即拉力小于重力的下滑分量,m1有下滑趋势,摩擦力沿切线向上,当达到最大静摩擦力时
![]()
解得:
![]()
因而当
![]()
半球体对m1的摩擦力的方向垂直于图中的虚线向上,故D正确。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目