Question

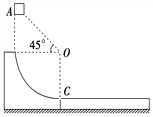
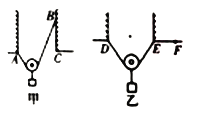
【题目】有甲、乙两根完全相同的轻绳，甲绳A、B两端按图甲的方式固定，然后将一挂有质量为M的重物的光滑轻质动滑轮挂于轻绳上，当滑轮静止后，设绳子的张力大小为T1；乙绳两端按图乙的方式连接，然后将同样的定滑轮且挂有质量为M的重物挂于乙轻绳上，当滑轮静止后，设乙绳子的张力大小为T2．现甲绳的B端缓慢向下移动至C点，乙绳的E端缓慢移动至F点，在两绳的移动过程中，下列说法正确的是（ ）

A. T1、T2都变大 B. T1变大、T2变小

C. T1、T2都不变 D. T1不变、T2变大

Answer 1

【答案】D

【解析】对甲图设绳子总长为L，两堵竖直墙之间的距离为S，左侧绳长为L1，右侧绳长为L2．由于绳子上的拉力处处相等，所以两绳与竖直方向夹角相等，设为θ，则由几何知识，得：S=L1sinθ+L2sinθ=（L1+L2）sinθ，又L1+L2=L
得到 ；
当绳子右端慢慢向下移时，S、L没有变化，则θ不变．绳子的拉力大小为T1，重物的重力为G．以滑轮为研究对象，根据平衡条件得2T1cosθ=G
解得： ；可见，当θ不变时，绳子拉力T1不变；
对乙图，当绳子的右端从E向F移动的过程中，由于绳子的长度不变，所以两个绳子之间的夹角增大，由于两个绳子的合力大小等于物体的重力，方向与重力的方向相反，所以当两个绳子之间的夹角增大时，绳子的拉力之间的夹角增大，所以绳子的拉力T2增大．故ABC错误，D正确．故选D.