题目内容
19.在一倾角为θ=37°的粗糙斜面上固定在水平面上,在斜面的底端固定一挡板,将一轻质弹簧固定在挡板处,可以视为质点的质量为m=1kg的物块与轻质弹簧不连接,并用外力作用于物体上将轻质弹簧压缩到某一位置,在t=0时刻将物块由静止释放,通过速度传感器在计算机上描绘出物块的v-t图象,如图所示,其中OA段为曲线,AB段为直线,0~0.1s的时间内物块沿斜面向上滑的距离为s=0.2m,g=10m/s2,sin37°=0.6,•=0.8,求:(1)斜面与物块之间的动摩擦因数μ;
(2)t=0时刻弹簧储存的弹性势能Ep.

分析 (1)物体离开弹簧后向上做匀减速运动,根据速度时间图线求出匀减速运动的加速度大小,结合牛顿第二定律求出动摩擦因数的大小.
(2)根据0.1s时的速度,结合上滑的距离,运用功能关系求出弹簧的弹性势能的大小.
解答 解:(1)由图象可知0.1s物体离开弹簧向上做匀减速运动,加速度的大小$a=\frac{△v}{△t}=\frac{2-1}{0.2-0.1}m/s{\;}^2=10m/s{\;}^2$
根据牛顿第二定律,有:mgsin37°+μmgcos37°=ma
解得:μ=0.5;
(2)由图线可知,t2=0.1s时的速度大小:v=2.0m/s
由功能关系可得:${E}_{p}=\frac{1}{2}m{v}^{2}+mgssin37°+μmgscos37°$
代入得:EP=4.0J;
答:(1)物体与斜面间的动摩擦因数μ的大小为0.5;
(2)压缩弹簧时,弹簧具有的弹性势能为4.0J.
点评 本题考查了牛顿第二定律、功能关系、以及运动学公式的综合,综合性较强,通过匀减速运动得出动摩擦因数是解决本题的关键.

练习册系列答案
相关题目
10. 如图所示,两材料完全相同的木块紧靠在一起,第一块的长度是第二块的两倍,固定在水平面上,一颗子弹以水平速度射入第一个木块,穿过第二个木块后的速度恰好为零,设子弹在两个木块中运动的加速度大小相等,则子弹刚射入两个木块时的速度之比v1:v2和穿过两个木块所用时间之比t1:t2分别为( )
如图所示,两材料完全相同的木块紧靠在一起,第一块的长度是第二块的两倍,固定在水平面上,一颗子弹以水平速度射入第一个木块,穿过第二个木块后的速度恰好为零,设子弹在两个木块中运动的加速度大小相等,则子弹刚射入两个木块时的速度之比v1:v2和穿过两个木块所用时间之比t1:t2分别为( )
 如图所示,两材料完全相同的木块紧靠在一起,第一块的长度是第二块的两倍,固定在水平面上,一颗子弹以水平速度射入第一个木块,穿过第二个木块后的速度恰好为零,设子弹在两个木块中运动的加速度大小相等,则子弹刚射入两个木块时的速度之比v1:v2和穿过两个木块所用时间之比t1:t2分别为( )
如图所示,两材料完全相同的木块紧靠在一起,第一块的长度是第二块的两倍,固定在水平面上,一颗子弹以水平速度射入第一个木块,穿过第二个木块后的速度恰好为零,设子弹在两个木块中运动的加速度大小相等,则子弹刚射入两个木块时的速度之比v1:v2和穿过两个木块所用时间之比t1:t2分别为( )| A. | v1:v2=2:1 | B. | v1:v2=$\sqrt{3}$:1 | C. | t1:t2=(1+$\sqrt{2}$):$\sqrt{3}$ | D. | t1:t2=($\sqrt{3}$-1):1 |
14.一质点沿x轴做直线运动,各个时刻的位置如表所示
则:第3s内的位移是1m,前3s内的位移为-3m,前5s内的路程为26m.
| t/s | 0 | 1 | 2 | 3 | 4 | 5 |
| x/m | 0 | 5 | -4 | -3 | -8 | -2 |
8.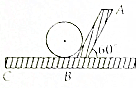 如图所示,水平台面上放着一个夹角为120°的支架ABC,质量为m的光滑球放在支架上静止不动,当支架以大小为a的加速度水平向左加速运动时,下列关于球的受力分析中正确的是( )
如图所示,水平台面上放着一个夹角为120°的支架ABC,质量为m的光滑球放在支架上静止不动,当支架以大小为a的加速度水平向左加速运动时,下列关于球的受力分析中正确的是( )
 如图所示,水平台面上放着一个夹角为120°的支架ABC,质量为m的光滑球放在支架上静止不动,当支架以大小为a的加速度水平向左加速运动时,下列关于球的受力分析中正确的是( )
如图所示,水平台面上放着一个夹角为120°的支架ABC,质量为m的光滑球放在支架上静止不动,当支架以大小为a的加速度水平向左加速运动时,下列关于球的受力分析中正确的是( )| A. | 球可能受4个力作用 | B. | 球一定受3个力作用 | ||
| C. | 球可能受2个力作用 | D. | 球一定受2个力作用 |
 如图所示,质量MA=2m的直杆A悬于离地面很高处,杆A上套有质量MB=m的小环B.将小环B由静止释放,环做加速度a=$\frac{3}{4}$g的匀加速运动.经过时间t后,将杆A上方的细线剪断,杆A开始下落.杆A足够长,环B始终未脱离杆A,不计空气阻力,已知重力加速度为g,求:
如图所示,质量MA=2m的直杆A悬于离地面很高处,杆A上套有质量MB=m的小环B.将小环B由静止释放,环做加速度a=$\frac{3}{4}$g的匀加速运动.经过时间t后,将杆A上方的细线剪断,杆A开始下落.杆A足够长,环B始终未脱离杆A,不计空气阻力,已知重力加速度为g,求: 为了让观众体会到亲身参与挑战的兴奋和激情,时下很多电视台推出了以全民体验竞技魅力为宗旨的大冲关节目.其中有一关叫跑步机跨栏,它的设置是先让观众通过一段平台,再冲上反向移动的跑步机,并在跑步机上通过几个跨栏,冲到这一关的终点.现有一套跑步机跨栏装置,平台长L1=4m,跑步机长L2=34m,跑步机上设置了一个跨栏(不随跑步机移动),跨栏到平台末端的距离L3=10m,且跑步机以v0=1m/s的速度匀速移动.一位挑战者在平台起点从静止开始,以a1=2m/s2的加速度通过平台,冲上跑步机,之后以a2=1m/s2的加速度在跑步机上向前冲.在跨栏后,以跨栏时的速度匀速通过剩余的路程.试求挑战者通过跑步机跨栏装置全程所需的时间是多少?
为了让观众体会到亲身参与挑战的兴奋和激情,时下很多电视台推出了以全民体验竞技魅力为宗旨的大冲关节目.其中有一关叫跑步机跨栏,它的设置是先让观众通过一段平台,再冲上反向移动的跑步机,并在跑步机上通过几个跨栏,冲到这一关的终点.现有一套跑步机跨栏装置,平台长L1=4m,跑步机长L2=34m,跑步机上设置了一个跨栏(不随跑步机移动),跨栏到平台末端的距离L3=10m,且跑步机以v0=1m/s的速度匀速移动.一位挑战者在平台起点从静止开始,以a1=2m/s2的加速度通过平台,冲上跑步机,之后以a2=1m/s2的加速度在跑步机上向前冲.在跨栏后,以跨栏时的速度匀速通过剩余的路程.试求挑战者通过跑步机跨栏装置全程所需的时间是多少?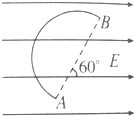 如图所示,带电荷量为-5×10-3C的点电荷在匀强电场中沿半径为10cm的半圆弧由A点运动到B点.已知电场强度E=1.0×103V/m,则此过程中电荷的电势能将如何变化?变化多大?
如图所示,带电荷量为-5×10-3C的点电荷在匀强电场中沿半径为10cm的半圆弧由A点运动到B点.已知电场强度E=1.0×103V/m,则此过程中电荷的电势能将如何变化?变化多大?